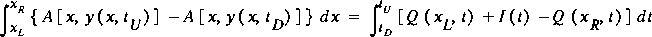.
Full Equations (FEQ) Model for the Solution of the Full, Dynamic Equations
of Motion for One-Dimensional Unsteady Flow in Open Channels and Through
Control Structures
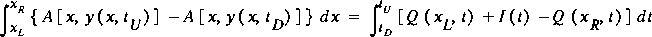.Dropping the wind-stress term, the integral form of the momentum-conservation equation for the same control volume is
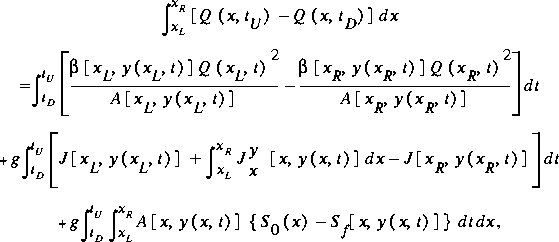
All the variables in equation 42 have been defined previously; but in this case, the dependence of these variables on location, x, time, t, and (or) water-surface height, y, is explicitly shown.
Equations 41 and 42 are in conservation form. If the water surface is discontinuous, these equations are still valid. However, the pressure-force terms involving the first moment of area and its rate of change at fixed water-surface height are cumbersome. Therefore, one can deviate slightly from the conservation form by requiring that the water-surface profile be continuous. In practice, this change has had negligible effects on results in simulating dam-break flood waves. By expressing the difference in the first moment of area at the ends of the control volume in differential form and by using the Leibniz rule to obtain an alternative form of the rate of change of the first moment of area with respect to distance, the momentum equation for the case of a continuous water-surface profile can be expressed without reference to the first moment of area as
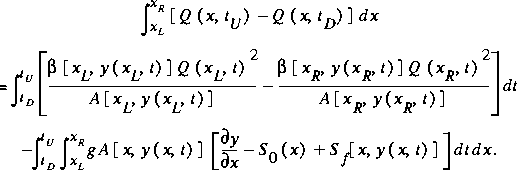
Taking into account that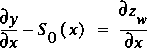 
, where zw = water-surface elevation, simplifies equation 43 to
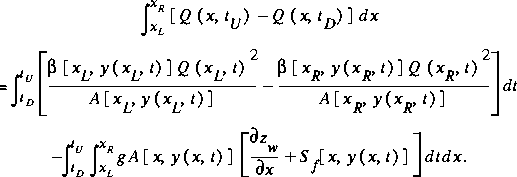
Any term in equations 41 and 44 requiring integration with respect to distance may require a weight coefficient when these equations are applied to a curvilinear stream channel. The weight coefficients for computing volumes and momentum content have been developed previously. Weight coefficients have been developed for equations similar to equations 41 and 44 by DeLong (1989) and Froehlich (1991). DeLong presented a momentum equation that did not include a weight coefficient on any term except the momentum-content term. Froehlich questioned this result and derived a correction factor for the friction term given by
,
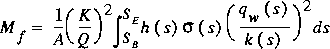where s is the offset distance across the cross section as measured from a reference point on the channel bank, h(s) is local depth in a cross section at cross-section offset s, qw(s) is the flow per unit width in a cross section at offset s, k(s) is the conveyance per unit width in a cross section at offset s,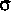 
(s) is the rate of change of distance along the flow line at offset s to the rate of change of distance along the channel axis (sinuosity at offset s), and sB and sE are the offset at the beginning and end of the wetted top width for the cross section. DeLong (1991) pointed out that the total conveyance applied by Froehlich (1991) was not adjusted for sinuosity and was computed assuming that the friction slope was the same for each flow line across the section. If the total conveyance is adjusted for sinuosity and the local conveyance adjusted for sinuosity is substituted into equation 45, then 
and, therefore, does not appear in the equations.
The omission of a weight factor on the pressure and gravity force terms in equations 41 and 44 may be surprising; however, as equation 44 indicates, the downstream force from these two terms is determined by the difference in water-surface elevation between two sections (that is, in the term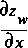 
). One of the fundamental assumptions for curvilinear and linear flow indicates that this difference is constant for each flow line between the two cross sections considered. Thus, the variation in the lengths of the flow-line distances makes no difference in solving these integrals. The assumptions applied to derive estimates of q(s), k(s), 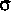(s), and the adjusted total conveyance are discussed in detail in Franz and Melching (1997).
Use of the results for the distance integrals in equation 44 and subsequent simplification yields
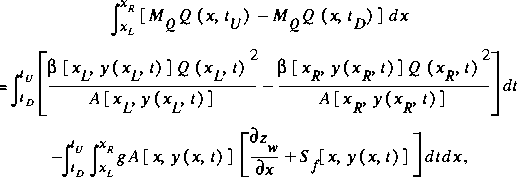
as the equation expressing momentum conservation in 1-D unsteady flow in curvilinear channels.
The mass conservation equation becomes
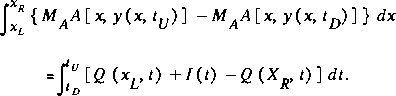
In equations 46 and 47, the arguments for the weight coefficients, MA and MQ, are omitted for simplicity. Definitions of MA and MQ are given in section 4.2.