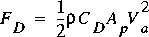[Next Section] [Previous Section] [Table of Contents]

Full Equations (FEQ) Model for the Solution of the Full, Dynamic Equations of Motion for One-Dimensional Unsteady Flow in Open Channels and Through Control Structures

U.S. GEOLOGICAL SURVEY WATER-RESOURCES INVESTIGATIONS REPORT 96-4240

5.5 Special Terms in the Equations of Motion

One-dimensional unsteady flow in an open channel can be simulated with the governing equations as given here; however, certain conditions in open channels require additional terms in the equations of motion. These conditions include the effects caused by diverging or converging channels and the effects of isolated obstructions, such as bridge piers or a pipe, in the flow. The latter effects can be isolated and treated separately from the governing equations, but it is often convenient to add to the governing equations the effect of simple submerged obstructions that do not exert appreciable control on the flow.

5.5.1 Drag for a Submerged Body

Because the momentum equation involves forces, any terms added to the motion equation must involve forces. The drag for a submerged body is

(48)

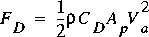where C_D is dimensionless drag coefficient depending on the nature of the submerged object and the flow; A_p is the area of the submerged object projected on a cross section orthogonal to the approach velocity; and V_a is the velocity of approach upstream from the submerged object.

In practical computations, V_a is taken as the average cross-sectional velocity in the computational element. The drag coefficient given earlier for the wind-stress term on the water surface included the factor for consistency with the source for wind-stress drag coefficients. Here, the traditional definition of the drag coefficient is retained. The projected area of the submerged object is a function of the water-surface elevation near the object. 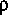Because the density, This is the Greek letter Rho , is constant, it does not appear in the final forms of the equations of motion in equations 31 and 46. Therefore, the density is also dropped from the drag equation for consistency with the final forms of the equation of motion. Thus, the adjusted drag becomes

(49)

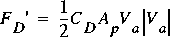where Equation has been replaced with 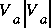so that the drag will always be opposite the flow.

The drag is considered to apply to a point within the control volume. The location of the drag-producing object, at 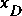Equation , is needed to define the water-surface height for estimating the projected area and the drag coefficient from the approaching flow. For simplicity, a single location is assumed to be adequate for both directions of flow. The approach-velocity source may vary with changes in direction of flow in the control volume; this is denoted by placing a subscript a on the location of the velocity. Thus, the full description at the adjusted drag is

(50)

5.5.2 Transformation of Energy-Head Losses to Drags for Control Structures

Representing the effect of a complex structure--a large trash rack, for example--may be necessary or desirable. Typically, the effect of such structures is given as a head loss (that is, in terms of mechanical energy) and is estimated by the product of a loss coefficient and the approach-velocity head. A head-loss term is incompatible with equation 46 because all terms in that equation refer to momentum content, momentum flux, or forces on the water in the control volume. The problem of incompatibility between momentum equations and energy losses arises because most past work in open-channel flow has used the principle of conservation of mechanical energy for control structures, in part because simpler equations result for certain steady flows. (This is not true for unsteady flow, as stated earlier.) The basic data used to derive the mechanical-energy-loss coefficients also could have been developed for the conservation of momentum principle. Thus, the mechanical-energy losses that are available must be transformed to yield reasonable estimates of drags that are suitable for use in the equation of motion. For convenience, the term here should be similar to that for an explicit drag so that both can be represented in the solution process in the same manner.

In applications of the mechanical-energy balance, head losses are commonly applied at points along a 1-D flow path even though these losses may take place over an appreciable length of the flow path. This is done for several reasons. First, the length over which the losses take place is only approximately known. Second, the manner in which the losses are distributed over this length is unknown. Third, the head losses are often small relative to the total head and other losses. Fourth, the length scales for the flow fields of interest are many times longer than the structures or channel features causing the head loss. Therefore, the distortion in concentrating a loss at a point is negligible. The transformation of the head loss to an equivalent drag needs to be located at a point in the control volume. In the derivation of this transformation in the equations of motion, the integral of the product of a slope and a cross-sectional area with respect to distance (when multiplied by g) gives a force term that applies to both the friction slope and the bottom slope. Thus, a slope, , is introduced to represent the loss of head, This is the Greek letter Delta h_p, in the control volume where

(51)

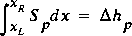If equation 51 is satisfied, then the drag, F_DE, that represents the effect of the head loss computed for the structure is given by

(52)

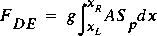F_DE is similar to the forces (gravity and boundary shear) computed with the other slopes in the equation of motion. By isolating the head-loss slope effect to the immediate vicinity of the obstruction at x_p and expressing the head loss as a fraction of the approach velocity head, the drag, F_DE, exerted on the flow by the obstruction at x_p may be expressed as

(53)

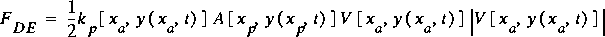where k_p is the head-loss coefficient for the obstruction at x_p. V|V| is used instead of V² in equation 53 because the drag is always opposite to the motion of the water.

A computational element in a channel may contain more than one simple structure, either constructed or natural, for which an estimated drag must be included in the momentum equation. For one simple structure (structure of type 1), it may be possible to estimate the drag from measured drag coefficients and the projected area of the structure, FD' computed with equation 50. For another simple structure (structure of type 2), it may be necessary to estimate the drag from an equivalent energy slope determined from a head-loss relation, F_DE' computed with equation 53. The total drag for the computational element is given by a single integral term over time (because equations 50 and 53 are of the same form) as

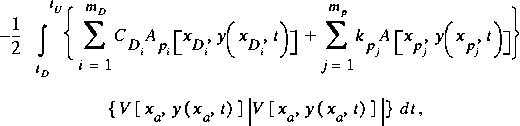
where m_D is the number of structures of type 1 present and m_p is the number of structures of type 2 present. The total drag given in the above expression is added to equation 46 to obtain the momentum equation for the computational element accounting for the localized drags resulting from simple structures.

If this transformation seems inappropriate, consider steady flow in a rectangular, prismatic, horizontal channel. Furthermore, assume that the friction losses are small relative to the local losses resulting from a large trash rack in the channel. The losses for trash racks are most often given in terms of a fraction of the approach-velocity head. If section 1 upstream from the rack and section 2 downstream from the rack are placed such that the 1-D assumptions are valid, then the principle of conservation of mechanical energy yields

(54)

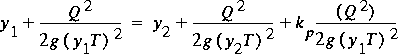as the equation relating the flow and water-surface height at sections 1 and 2, y₁ and y₂, respectively. Application of the principle of conservation of momentum yields

(55)

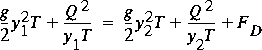as another equation relating the flow and water-surface height at sections 1 and 2. For a given flow and approach water-surface height, equation 54 gives the water-surface height at section 2. Substitution of these water-surface heights into equation 55 gives a value for the drag. Equation 53 also gives an estimate of the drag.

How well does equation 53 represent the drag computed for this simple but physically realistic example? To answer this question, the Froude number for the approaching flow,

(56)

;

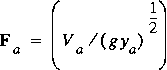the ratio of downstream water-surface height to upstream water-surface height, 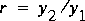; and the drag rescaled by the upstream hydrostatic-pressure force, 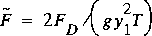are used to convert the equations to a dimensionless form,

(57)

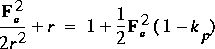for the energy relation, and

(58)

for the momentum relation. An estimate of drag is computed by solving equation 56 for the water-surface height ratio given the Froude number and the loss coefficient and substituting the ratio into equation 57 to estimate the dimensionless drag, 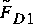. If equation 53 is applied in equation 55, the dimensionless form becomes

(59)

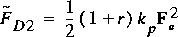provided that the proper area is the arithmetic average of the area upstream and downstream from the trash rack or other structure. Equation 58 defines another dimensionless drag. How does the value of 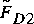compare with 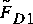, the best estimate of the drag? The absolute value of the relative error in dimensionless drag force, 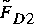, taking 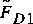as the correct value is shown in table 2.

The largest error in table 2 is about 4 percent when the approach Froude number and loss coefficient are such that the Froude number at the downstream section is between 0.95 and 1. When the downstream flow is clearly subcritical, the error is less than 1 percent for a wide range of flow conditions. Therefore, application of equation 53 provides a close estimate of the drag in any reasonable flow, and the area to use is the arithmetic average of the areas in the cross sections bounding the location of the loss.

5.5.3 Sudden Cross-Sectional Expansions or Contractions

The effect of converging and diverging channels on the flow is complex. Again, these effects are typically expressed in terms of a head loss. The losses for diverging channels are larger than those for converging channels. When the velocities are decreasing in the direction of the flow, turbulence is increased, and the water adjacent to the sides of the channel may separate from the sides and form large eddies. The distribution of velocity becomes highly nonuniform and is no longer predominantly affected by the shape of the boundary of the channel. When the velocities are increasing in the direction of flow, the velocity becomes more nearly uniform and turbulence is reduced. Estimation of these losses is difficult, and empirical relations are used for loss estimation. See the discussion of the EXPCON command in the FEQUTL documentation report (Franz and Melching, 1997) for a more extensive discussion of these difficulties.

The empirical relation applied to estimate head losses in expansions or contractions takes a fraction of the absolute value of the velocity-head difference over the length of the divergence or convergence. This relation was developed for designed and constructed transitions in canals where transitions are relatively short and infrequent. The same relation has been used in natural channels with irregular variations in size and shape. These irregular natural variations reduce the accuracy of the empirical relation for head-loss estimation, but there are no practical alternatives. Therefore, the velocity-head difference over the length of the control volume is taken in the derivation here.

The head losses resulting from flow separation from the sides of the channel, sometimes called eddy losses, are in excess of head losses resulting from boundary friction. The values of Manning's n given in various tabulations are presumed to exclude these eddy losses and, therefore, represent only the frictional effects in mostly straight prismatic channel sections. This means that estimates of Manning's n in natural channels derived from measurements in the channel must be treated carefully. The value of Manning's n could differ in response to how the eddy losses were estimated. Available steady-flow water-surface-profile computer programs, supported by various Federal agencies, differ in treating these losses. Thus, if each of the computer programs was used to estimate Manning's n from a set of careful measurements in a natural channel, different results would be produced merely because of differences in the treatment of minor losses.

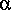Further issues must be addressed before the head-loss equations can be presented. The standard head-loss equation for expansions and contractions was developed for channels that are compact in shape; that is, channels where . Therefore, potential effects of large values of This is the Greek letter Alpha for natural channels are not discussed. Inclusion of a values will require additional values in the cross-section tables when the governing equations for a branch are approximated. In addition, the variation in the energy-flux-correction coefficients, 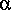, over the distance of a typical computational element is generally small. Furthermore, uncertainties in the estimation of the eddy losses are large. Therefore, it seems reasonable to exclude 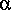This is the Greek letter Alpha in the equations applied to estimate the eddy losses to simplify the computation. The effect of 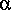can be partially reflected by increasing the fraction of the velocity-head difference used to estimate the loss. Alternatively, the roughness values in the cross-section description can be changed to reflect the eddy losses (for an example, see Chow, 1959, p. 267). If the change in cross section is large over a short distance, then the transition should be isolated and treated as a special feature so that a more comprehensive evaluation of the losses can be computed.

On the basis of the assumptions discussed above, the head loss for accelerating or decelerating flow is

(60)

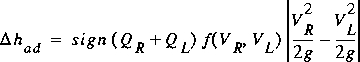where

(61)

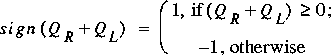
(62)

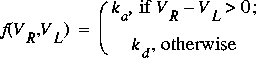
k_a is coefficient for accelerating flow, k_d is the loss coefficient for decelerating flow, and the subscripts L and R refer to the left and right ends of the control volume. Again, the loss must change sign so that the flow will always be retarded. Because this loss is assumed to apply over the control volume, another assumption is required to determine the direction of flow for the control volume. The direction of flow is determined in equation 59 on the basis of the sum of flows at each end of the control volume.

In cases where flow reversal is possible (for example, in tide-affected reaches) the sum of flows for a flow element may be zero because flow is either entering both ends or leaving both ends. When the flow is entering the control volume from both ends, a loss for deceleration is assigned, whereas when the flow is leaving from both ends of the control volume, a loss for acceleration is assigned. This convention seems reasonable because the turbulence present when the flow is entering from both ends would be larger than when it is leaving from both ends.

The slope of the eddy loss distributed over the length of the control volume, S_ad, can be defined as

(63)

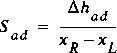This slope is analogous to the friction slope and must be added in a similar position and with the same sign.

5.5.1 Drag for a Submerged Body
5.5.2 Transformation of Energy-Head Losses to Drags for Control Structures
5.5.3 Sudden Cross-Sectional Expansions or Contractions

[Next Section] [Previous Section] [Table of Contents]