[Next Section]
[Previous Section]
[Table of Contents]
Full Equations Utilities (FEQUTL) Model for the Approximation of
Hydraulic Characteristics of Open Channels and Control Structures During
Unsteady Flow
U.S. GEOLOGICAL SURVEY WATER-RESOURCES INVESTIGATIONS REPORT 97-4037
4.2 Culverts
The flows through culverts are computed in FEQUTL by using peak-flow
estimation methods developed by the USGS as outlined in Bodhaine
(1968). The principles given by Bodhaine for the routing technique
are applied in the CULVERT command (section
5.5) to compute 2-D tables of type 13 for a culvert with or without
flow over the roadway. The cross-section locations used in the routing
analysis are shown in figure 3. The approach
section, section 1 in figure 3, is at least one culvert-opening width upstream
from the entrance to the culvert. Section 2 is the cross section of the
culvert barrel at the culvert-barrel entrance. Section 3 is the cross section
of the culvert barrel at the culvert-barrel exit. The departure section,
section 4, is usually located where the distribution of velocity in the
stream has essentially returned to the distribution resulting if the culvert
were not present. This location shifts with changes in flow and is a complex
function of poorly understood factors. Therefore, in practical terms, the
section represents the shape of the stream one opening width or more downstream
from the culvert-barrel exit. In FEQ simulation, section 1 is the cross
section at the downstream end of the branch upstream from the culvert,
and section 4 is the cross section at the upstream end of the branch downstream
from the culvert. Thus, the flow through the culvert is computed in the
CULVERT command in FEQUTL for a range of water-surface elevations at section
1 and section 4. The other sections are applied only in FEQUTL computations
and are not applied in FEQ simulation. In FEQUTL applications, the length
of stream between sections 1 and 2 is called the approach reach and the
length of stream between sections 3 and 4 is called the departure reach.
4.2.1 Additional Flow Types
Flow through culverts is one of the more complex steady-flow phenomena
encountered in the application of one-dimensional flow techniques. Bodhaine
(1968) defined six flow types for flow through culverts, summarized
in table 3, to determine peak discharges at culverts on the basis of high-water
marks and culvert geometry. Three of these flow types (1, 2, and 3) are
for low-head flow, two are for high-head flow (5 and 6), and one is for
the case where both the culvert inlet and exit are submerged (4).
Bodhaine (1968) defined the
boundary between high-head and low-head flow as (zw1-zci)/
D = 1.5 where zw1 is the water-surface elevation
in the approach section (section 1 in fig.3),
z ci is the elevation of the culvert invert at the downstream
end, and D is the maximum inside vertical dimension of the culvert
barrel. Chow (1959, p. 493) noted
that the change between high-head and low-head flow (culvert entrance submerged
or not submerged) may result for (zw1-zci)/
D as small as 1.2 depending on the geometry, barrel characteristics,
and approach condition. Chow states that for preliminary analysis (zw1-zci)/
D 1.5 may be used because computations have shown
that, where submergence was uncertain, greater accuracy can be obtained
by assuming that the entrance is not submerged (low-head flow). However,
for routing of unsteady flow through the culvert, a more explicit consideration
of the transition region is necessary. As a specific example, Bodhaine
(1968, p.47) noted that, for a range of approach water-surface elevations,
the designation of the flow as low head (flow type 1) or high head (flow
type 5) is unstable. Laboratory data indicate that the unstable condition
begins at (zw1-zci)/ D = 1.2, where
the flow is usually low head, and ends at (zw1-zci)/
D = 1.5, where the flow usually becomes high head. Bodhaine
(1968) recommended that the culvert discharge rating in this range
of approach water-surface elevations between flow types 1 and 5 be represented
by a straight line between the discharge computed with low-head methods
at a ratio of 1.2 and the discharge computed with high-head methods at
a ratio of 1.5.
1.5 may be used because computations have shown
that, where submergence was uncertain, greater accuracy can be obtained
by assuming that the entrance is not submerged (low-head flow). However,
for routing of unsteady flow through the culvert, a more explicit consideration
of the transition region is necessary. As a specific example, Bodhaine
(1968, p.47) noted that, for a range of approach water-surface elevations,
the designation of the flow as low head (flow type 1) or high head (flow
type 5) is unstable. Laboratory data indicate that the unstable condition
begins at (zw1-zci)/ D = 1.2, where
the flow is usually low head, and ends at (zw1-zci)/
D = 1.5, where the flow usually becomes high head. Bodhaine
(1968) recommended that the culvert discharge rating in this range
of approach water-surface elevations between flow types 1 and 5 be represented
by a straight line between the discharge computed with low-head methods
at a ratio of 1.2 and the discharge computed with high-head methods at
a ratio of 1.5.
Tables of type 13 are computed with FEQUTL to represent the flow through
culverts and to be applied as internal boundary conditions in the unsteady-flow
simulation in FEQ. Tables of type 13 contain flow rate as a function of
upstream and downstream water-surface elevations. These tables are computed
as follows. Initially the upstream and downstream water-surface elevations
are identical and no flow results. Then the downstream water-surface elevation
is lowered (as per a user-specified series of partial free drops) and at
the same time the flow rate is increased from the initial zero flow so
that the upstream water-surface elevation is maintained. As the downstream
water-surface elevation continues to lower, the flow increases to maintain
the upstream water-surface elevation. This computational procedure precludes
the use of the method recommended by Bodhaine
(1968) because in his method the flow rates for (zw1-zci)/
D equal to 1.5 and 1.2 are computed for a fixed downstream water-surface
elevation. Then the linear interpolation is applied on the flow rate for
the actual value of (zw1-zci)/ D, whereas
flow rates are computed for fixed, upstream water-surface elevation and
variable, downstream water-surface elevation in FEQUTL. Thus, special additional
flow types [relative to the six flow types identified by Bodhaine
(1968)] must be defined and used in FEQUTL to simulate flow in the
range of upstream water-surface elevations between flow types 1 and 5.
The need for special additional flow types to simulate the flow between
low-head and high-head flow types 1 and 5 results from physical oscillations
for a range of upstream water-surface elevations. Other special additional
flow types are needed to approximate flow in the vicinity of changes between
high-head flow types, low-head and high-head flow types, and submerged
flow (type 4) and low-head or high-head flow. These special flow types
do not necessarily result in a real stream system, but rather these flow
types may be needed to circumvent computational problems at transitions
between flow types in FEQ simulation of unsteady flow. For example, as
flows in culverts change between free-surface and pressurized conditions,
a discontinuity in the flow results. The numerical methods applied in FEQ
to route unsteady flows through the stream system may not be capable of
obtaining a solution for flows or water-surface heights at an internal
boundary condition if a large discontinuity in the flow rating is present.
Therefore, special flow types are included in FEQUTL to circumvent discontinuities
in the internal boundary conditions at culverts. The flow conditions described
with the additional flow types may be present only for short periods as
a flood wave passes through the culvert or backwater extends from downstream
locations. As detailed in later sections, not all transitions between flow
types involve substantial flow discontinuities; thus, not all changes between
flow types are considered in FEQUTL. The actual transition between flow
types as upstream and downstream water-surface elevations change during
unsteady flow are simulated in FEQ by look-up among the tables of type
13 representing the various upstream and downstream water-surface elevations.
Special additional flow types also are needed because simulation of
unsteady flow in streams requires flow to be defined for a wide range of
flows, from small to large, and not just the large design flows considered
by Bodhaine (1968).
The additional flow types defined in FEQUTL to describe a wider range
of flow conditions than included in the six flow types defined by Bodhaine
(1968) are designated flow types 0, 31, 41, 42, 51, 52, 61, 62, and
7. These are described in table 3 and illustrated in figures 4-11.(figs.
4 and 5),(figs. 6 and 7),(figs.
8 and 9),(figs. 10 and 11). The designations
of entrance and exit in table 3
refer to the direction water is flowing, not the direction that is the
predominant or expected direction. The nature of flow in the culvert is
described as free or submerged in table 3.
Submerged indicates that no critical control is present in
the structure because it is drowned by backwater effects. For example,
flow type 4, defined by Bodhaine (1968),
is obviously submerged because both ends of the culvert are underwater.
Flow type 3, defined by Bodhaine (1968),
also is submerged because the downstream water-surface elevation is greater
than the elevation of critical depth in the culvert. Each of the other
flow types defined by Bodhaine (1968)
is free flow. This designation is less explicit than Bodhaine's
(1968) designation of flow in culverts as critical, subcritical, supercritical,
and full barrel or critical, tranquil, rapid, and full barrel because some
of the special additional flow types are intermediate conditions between
subcritical and supercritical flows and may be either type of flow, depending
on hydraulic and geometric conditions of the culvert. For the computations
in FEQUTL, a more precise definition of flow regime is not necessary. Further,
this designation is consistent with that for free and submerged weir and
orifice flow for underflow gates (section
4.8).
At large flows, culverts almost always cause a contraction of the flow
at the entrance and an expansion of flow at the exit. This is the standard
assumption for analysis of culverts. However, at low to moderate flows,
culverts can provide an expansion of flow at the entrance and a contraction
of flow at the exit. Such conditions are considered in flow types 0 and
7. In flow type 0, the control is the approach section. At a given upstream
water-surface elevation (upstream head), the capacity of the culvert is
such that critical flow is present at the approach section. In flow type
7, the control is at the departure section so that critical control is
present such as may result from a riffle in the stream channel downstream
from the culvert during low flow. Flow type 31 results when flow types
1 or 2 in long culverts are submerged. In this case the exit can be submerged
but the entrance has a free surface.
A flow of type 6 results in a piezometric surface at the culvert exit
that is below the soffit (the highest point in the culvert at a given location)
of the culvert at that point. When the piezometric surface in the departure
reach for flow type 6 is drowned but the soffit is under free-flow conditions
(that is, not submerged) the flow is designated as type 42 in FEQUTL. This
could result from submergence of the control for flow types 6 or 62. Flow
type 61 only results for flow against an adverse slope. For this flow type,
the culvert is flowing full at the inlet but is flowing partially full
at critical depth at the outlet. Submergence of flow type 61 can result
in flow type 41. Flow type 41 also is a transition between flow types 3
and 4. Flow type 62 is transitional and is used to smooth the transition
between the low-head flow types 1 and 2 and the high-head flow type 6. Flow
type 62 also is used as a transitional flow type between flow types 61
and 6. Flow types 51 and 52 provide transitions between flow types 1 and
5 and flow types 2 and 5, respectively. Typical flow profiles for the additional
flow types are shown in figures 4-11.
(figs.
4 and 5),(figs. 6 and 7),(figs.
8 and 9),(figs. 10 and 11)
4.2.2 General Routing Methodology for Culvert Flow
The routing methodology defined by Bodhaine
(1968) starts at a control point or at a known water-surface elevation,
and a steady-flow energy-conservation equation from that point is applied
to define the unknown flow and elevation values. The equations that result
fall into three groups: flow type 1, flow types 2 and 3, and flow types
4 and 6.
For culvert-flow type 1, the control is at the culvert entrance (section
2). The coefficient of discharge, C d, in this case does
not represent appreciable energy losses because the flow is contracting
into the culvert entrance. The loss of energy is caused by subsequent expansion
in the culvert barrel that results downstream from section 2. Therefore,
the coefficient of discharge may be determined by applying
(83)
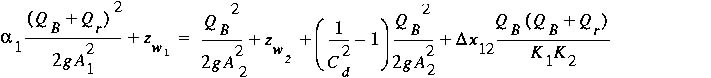
where
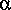 1 1 |
is the kinetic-energy flux correction coefficient at section 1
(the approach section);
|
| Q B |
is the flow in the culvert barrel; |
| Q r |
is the flow over the roadway; |
| g |
is acceleration due to gravity; |
| A i |
is the flow area at section i; |
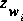 |
is the water-surface elevation at section i; |
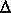 x 12 x 12 |
is the distance between sections 1 and 2; |
| K i |
is the conveyance at section i; |
and the critical flow at section 2 is given by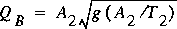 .
.
The flow rate at section 2 is critical with the water-surface elevation
at section 2,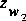 , being the water-surface elevation at critical flow. This equation is
solved iteratively starting with an initial estimate of the critical depth
at section 2. The iteration continues until the known elevation at section
1,
, being the water-surface elevation at critical flow. This equation is
solved iteratively starting with an initial estimate of the critical depth
at section 2. The iteration continues until the known elevation at section
1,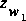 , is matched to an acceptable tolerance criterion.
, is matched to an acceptable tolerance criterion.
For culvert-flow types 2 and 3 the energy equation is
(84)
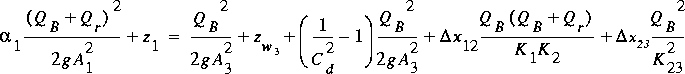 ,
,
where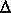 x23 is the length
of the culvert and K23 is the average value of conveyance
for the culvert that gives the correct barrel-friction loss computed in
the steady-flow profile computations. The barrel friction loss and the
conditions at section 2 are estimated by computing a steady-flow water-surface
profile in the culvert barrel. The entrance losses,
x23 is the length
of the culvert and K23 is the average value of conveyance
for the culvert that gives the correct barrel-friction loss computed in
the steady-flow profile computations. The barrel friction loss and the
conditions at section 2 are estimated by computing a steady-flow water-surface
profile in the culvert barrel. The entrance losses,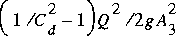 , are assigned to the barrel so that the estimated water-surface elevation
at section 2 reflects the expansion losses that take place in the barrel
downstream from the entrance. These losses may not be fully realized if
the barrel is short. This refinement is not included in the CULVERT command
because the factors involved are not well defined. Therefore, a warning
message is given if the culvert is clearly too short, usually defined as
a length less than six times the maximum inside the vertical dimension,
D.
, are assigned to the barrel so that the estimated water-surface elevation
at section 2 reflects the expansion losses that take place in the barrel
downstream from the entrance. These losses may not be fully realized if
the barrel is short. This refinement is not included in the CULVERT command
because the factors involved are not well defined. Therefore, a warning
message is given if the culvert is clearly too short, usually defined as
a length less than six times the maximum inside the vertical dimension,
D.
For culvert-flow type 2, the flow at the outlet of the conduit (section
3) is critical, but for culvert-flow type 3, the flow is subcritical throughout
the conduit. Equation 84 is solved iteratively for the water-surface elevation
at section 1 given either that the flow at section 2 is critical or given
a water-surface elevation at the culvert exit (section 3),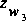 .
.
For culvert-flow types 4 and 6, the energy equation is
(85)
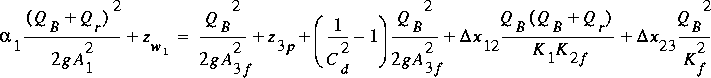 ,
,
where z 3p is the elevation of the piezometric surface
at section 3 and the f in subscripts denotes the full-flow value
for the culvert barrel. This equation must be solved iteratively for culvert-flow
type 6 because the piezometric level at section 3 is a function of the
flow in the culvert barrel as shown in figure
18 in Bodhaine (1968). For
culvert-flow type 4, equation 85 may be solved directly for the flow because
in this case the piezometric level at section 3 is given. This direct solution
is only possible if no flow over the road results. If flow over the road
results, iteration is required.
The flow over the road is defined by the water-surface elevation at
section 1, the upstream water level for weir flow over the road. The downstream
water-surface elevation for the flow over the road is taken at section
43 (fig. 3). The downstream water-surface elevation
for flow through the culvert also is defined at section 43. Under submerged
flow conditions (flow type 4) the piezometric levels at sections 3 and
43 are identical. The flow over the road is computed using the same methods
as for embankments and other weirs (section
4.3). The effect of approach velocity head on the flow over a weir
is included on a local basis. The approach conditions for the flow at a
point on the weir crest are estimated upstream from that point and not
for the approach of the entire cross section. This is done because flows
over a road commonly take place during floods, and the approach conditions
to the road are usually on the flood plain of the stream. The velocity
head on the flood plain can be substantially different from the velocity
head in the stream channel at the culvert or bridge. Flow over the road
directly above the culvert is normally a small part of the total flow over
the road. Often, guard rails or other obstructions to flow above the culvert
further reduce the effectiveness of the flow path directly above the culvert.
Furthermore, no laboratory or field data are available on the nature of
the interaction between flow through the culvert opening and flow over
the road directly above the culvert. Consequently, in the CULVERT command
the velocity head induced at section 1 by the flow through the culvert
is assumed to have a negligible effect on the flow over the road. Therefore,
the flow over the road, for free-flow conditions, is computed from the
water-surface elevation at section 1, independently of the flow through
the culvert.
Transitional-flow profiles are computed with variations on equations
83-85. For example, culvert-flow type 61 is computed with an equation
like that for culvert-flow type 2 (equation
84), except that the entrance flows full, the culvert barrel is full
along part of its length, and the coefficient of discharge differs from
that for type 2. The Preissmann
(1961) slot technique is applied in the CULVERT command to represent
pressurized flows as free- surface flows. Water-surface profiles in the
barrel that are a combination of full flow and part-full flow are computed
by allowing the section to flow full with the water level in the slot giving
the piezometric level in the full-flow part of the barrel. The other nonstandard
flow types (41, 51, 52, and 62) are computed in a similar manner.
4.2.3 Routing Methodology for Culvert-Flow Type 5
The representation for flow type 5 in
Bodhaine (1968) does not permit the application of a routing methodology.
This cannot be applied in the CULVERT command. All culvert-flow types can
be submerged given sufficient downstream water-surface elevations. Therefore,
culvert-flow type 5 must be computed so that it can be merged with the
other culvert-flow types.
Type 5 flow is analogous to free flow under a sluice gate. The entrance
to the culvert is flowing full, but the water surface becomes free of the
culvert soffit and an air space is present above the water surface from
the entrance to the exit. The nature of the rounding and beveling of the
culvert has a marked effect on type 5 flow. The flow in the culvert barrel
contracts to a minimum area (vena contracta) at about three vertical diameters
from the entrance (Portland Cement
Association, 1964, p. 111). Downstream from the vena contracta, flow
expansion takes place with losses similar to those for full-barrel flow
for the same entrance condition. The discharge coefficients for culvert-flow
type 5 relate primarily to the reduction in area and not the loss of energy.
The loss of energy, as in culvert-flow type 1, takes place downstream from
the vena contracta. The flow at the vena contracta is supercritical. The
depth downstream from the vena contracta may increase or decrease, depending
on the slope and roughness of the barrel.
Submergence of type 5 flow cannot be separated from the transition to
full-barrel flow. For the part-full flow to persist during flow transitions,
an adequate flow of air into the space above the water surface must be
present. The high velocities normally present in culvert-flow type 5 are
quite effective in moving and entraining air. If the barrel is long enough
and the water level or velocity is high enough, the air stream entering
the culvert along the soffit will encounter enough resistance to reduce
the pressure in the space above the water surface close to the inlet, resulting
in full flow at the culvert entrance. Once initiated, the full-flow region
will rapidly fill the remainder of the culvert. The flow rate immediately
increases, and this increase may lead to air entrainment through vortices
at the culvert inlet. Part-full flow may then result because of the entrained
air. The flow will oscillate between part-full and full flow until the
water level at the entrance rises too high for sufficient air to be entrained
by the vortices.
The ventilation of the culvert barrel can also be reduced by a rising
tail-water level that results in a hydraulic jump in the barrel exit. Eventually,
the face of the jump will come close enough to the exit soffit to restrict
the air flow sufficiently to result in full flow. This full-flow value
is assumed to be a submerged flow value in FEQUTL. It may be possible that
submergence of a culvert-flow type 5 may result in a culvert-flow type
6 that is unsubmerged. Insufficient data are available to determine under
what conditions an unsubmerged culvert-flow type 6 could result from submergence
of culvert-flow type 5.
A hydraulic jump commonly will start in the culvert barrel and end at
some point in the departure reach. A sketch of the location of the jump
and the sections is shown in figure 12. As
the water-surface elevation at the departure section and the section at
the end of the jump (sections 4 and 44) increases, the jump moves farther
into the barrel. To estimate the water-surface elevation at sections 4
and 44 that results in full flow in the barrel, a modified, simple momentum
balance is utilized. The hydrostatic, piezometric level at section 43 is
sought. The pressure distribution at section 43 is not hydrostatic because
parts of section 43 are in a hydraulic jump. However, the pressure on the
downstream face of a hypothetical head wall at the culvert outlet would
be approximately hydrostatic. Thus, the full-flow-inducing depth is defined
in terms of hydrostatic, piezometric head because it is not possible to
compute any other level by applying simple equations. The modified momentum
balance equation for the departure reach is
(86)
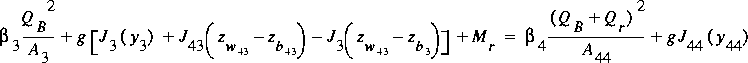 ,
,
where M r is the momentum flux over the roadway and
the subscript b denotes the invert elevation at the given section,
and J ( X f ) indicates that the first moment
of area with respect to the water surface is a function of X f.
The flow at section 3 is supercritical, so the depth and flow there are
known from the computations of culvert-flow type 5.
The downstream water-surface elevation resulting in full flow for culvert-flow
type 5 and that resulting in submergence of culvert-flow type 5 are taken
to be identical. Thus, the submergence can be defined if the flow and depth
at section 3 can be estimated. The discharge equation for culvert-flow
type 5, given in Bodhaine (1968),
is
(87)
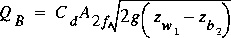 .
.
The velocity head of approach is assumed to be negligible in equation
87. This may be reasonable because culvert-flow type 5 under high-head conditions
is not efficient. Friction losses in the approach reach are also not considered
in equation 87. The details of the location and size of the vena contracta
are implicit in equation 87. An energy equation between section 1 and the
vena contracta can be written as
(88)
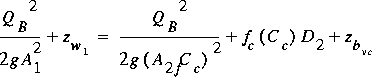 ,
,
where
| C c |
is the contraction coefficient on the full barrel area giving the flow
area at the vena contracta; |
| f c ( C c
) |
is the piezometric depth ratio to the maximum vertical dimension as
a function of the contraction coefficient; and |
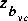 |
is the invert elevation at the vena contracta. |
A simple way to define the function f c is to assume
that the piezometric depth is the same as the depth to vertical diameter
ratio that defines the contracted area. This function is then determined
once the barrel cross-sectional shape is defined. For example, if C
c is 0.5, then for a circular culvert, the depth ratio is
also the same. In a box culvert, the partial-depth ratio and the partial-area
ratio are the same. The partial-depth ratio and partial-area ratio deviate
from each other for other shapes. The assumption that this applies to the
piezometric depth is only approximate. The contraction at the entrance
is predominantly from the soffit, but there also are contractions from
the sides of the culvert entrance. The effective flow area at the vena
contracta is probably less than the area of water at the vena contracta.
The simple assumption applied in FEQUTL is that the effective flow area
and the area containing water are the same.
The contraction coefficient is defined by requiring that the flow in
equations 87 and 88 be the same. These two equations define a contraction
coefficient for a given water-surface elevation at section 1 and a given
discharge coefficient for culvert-flow type 5. A contraction coefficient
for culvert-flow type 5 is determined in the CULVERT command whenever required.
Once the contraction coefficient is defined, it is applied in an equation
without the assumptions made for equation
87. The equation for culvert-flow type 5 then becomes
(89)
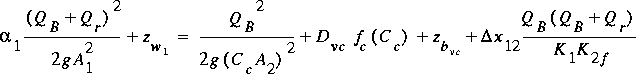 ,
,
where D vc is the maximum inside vertical dimension
of a culvert barrel at the vena contracta. This equation yields slightly
different results than the defining equation
(equation 87), but the differences are small when both equations are
applicable.
Most of the expansion losses in part-full flow take place close to the
vena contracta. These losses are assumed to be the same as for culvert-flow
type 6 at the same flow rate but at full flow. It is further assumed that
the losses are realized over a distance of three culvert diameters downstream
from the vena contracta, which is located three culvert diameters downstream
from the culvert entrance. Experience with FEQUTL has indicated that application
of the full culvert-flow type 6 losses sometimes result in failure of supercritical-profile
computations when no physical reason for failure is present. In these cases,
the estimated losses are reduced iteratively by 0.95 until the losses are
small enough to permit computation of the supercritical profile.
During computation of a 2-D culvert-rating table in FEQUTL, a procedure
must be specified to determine which high-head culvert-flow type, 5 or
6, is present. The slope, length, roughness, and entrance condition of
the culvert are all factors that affect the presence of culvert-flow type
5 or 6. Bodhaine (1968) prepared
two figures to aid in the determination of whether high-head culvert-flow
is type 5 or type 6. Bodhaine's figure for pipe or box culverts with a
smooth surface (concrete or similar material) is presented in figure
13, and his figure for pipe culverts with rough barrels is presented
in figure 14. The first estimate of the culvert-flow
type for high-head flow is given in these figures. If the culvert-flow type
selected is type 6, computations for culvert-flow type 6 proceed. However,
if the culvert-flow type selected is type 5, further checking of flow conditions
is done in FEQUTL.
Culvert flow type 5 must be verified and a full-flow-inducing depth must
be assigned at the culvert exit. Verification is important because the
classification of culvert-flow types in figures
13 and 14 is only approximate and many
culverts fall outside the range of the figures. The tables in FEQUTL that
represent these figures have been extended to accommodate a larger range
of culverts. However, this extension is an extrapolation and does not involve
any new data or computations. Furthermore, culverts have a tendency to
flow full, as discussed in Portland
Cement Association (1964, p. 98-99). Therefore, the decision rules programmed
in FEQUTL result in culvert-flow type 6 more often than culvert-flow type
5.
The following steps are completed in FEQUTL to verify culvert-flow type
5.
-
Starting at the vena contracta, a supercritical flow profile is computed
to the culvert exit. If the culvert is shorter than three culvert diameters,
then the vena contracta is treated as if it is at the entrance. This profile
may not extend to the exit because a hydraulic jump forms at some point
in the barrel.
-
A subcritical profile is computed from the culvert exit to the vena contracta
starting at critical depth for culvert-flow type 5. This profile may not
result, may result part way, or may extend to the vena contracta.
-
A simple momentum balance is applied between the subcritical and supercritical
profiles to locate any hydraulic jump. If no jump is present and supercritical
flow is present throughout the culvert, then culvert-flow type 5 is applied.
If subcritical flow is present throughout the culvert, then culvert-flow
type 5 is rejected.
-
If a jump is present, culvert-flow type 5 is rejected if the estimated
depth of flow on the downstream side of the jump is more than 0.8 D. Hydraulic
jumps in these cases would probably have substantial waves on the subcritical
side. Thus, any close approach to the barrel soffit would effectively seal
the air space and culvert-flow type 5 would not result.
A full-flow-inducing depth value at the exit of the culvert barrel is assigned
in FEQUTL as follows. This value is computed to determine what flow conditions
must be present to establish a transition from culvert-flow type 5 to type
6. The goal of completing the following eight steps is to define a full-flow-inducing
depth that is consistent with the culvert-flow type 5. If this is not done,
the results will be in error or the computations that follow might fail.
-
The value of rounding/beveling necessary so that the culvert would be on
the boundary between flow types in figures 13
and 14 is computed. If the rounding or beveling
is already at or above the maximum value given in those figures, a user-assigned
parameter defining the ratio of the full-flow-inducing depth at the exit
to D at the exit, TY5SBF, is applied. The default value of TY5SBF determined
from engineering judgment is 0.75.
-
The discharge coefficient corresponding to the enhanced rounding/beveling,
determined in step 1, is determined from table 6 in Bodhaine
(1968), which is included in the TYPE5.TAB input file for FEQUTL. Utilizing
this discharge coefficient the type 5 flow for the enhanced rounding/beveling
is computed.
-
The computations for verification of the culvert-flow type 5, outlined
above, are done to define the nature of the water-surface profile resulting
for the flow computed for the enhanced rounding/beveling.
-
If the prevailing profile at the flow computed for the enhanced rounding/beveling
is subcritical or includes a hydraulic jump that has a downstream depth
greater than 0.8 D, the enhanced rounding/beveling is reduced and the value
for flow computed for the new enhanced rounding/beveling is reduced. This
is done in steps of one-eighth of the difference between the enhanced rounding/beveling
and the actual rounding/beveling value in FEQUTL. If no meaningful flow
profile corresponding to the enhanced rounding/beveling can be found in
this process, type 5 flow is rejected. An acceptable enhanced profile must
have a rounding/beveling value greater than the actual rounding/beveling
value and must result in supercritical flow or a hydraulic jump in the
culvert with a downstream depth less than 0.8 D.
-
If both the actual profile and the profile corresponding to the flow computed
for the enhanced rounding/beveling are supercritical and extend through
the length of the culvert, then the end depth from the enhanced profile
is taken as the full-flow-inducing depth.
-
If the actual profile includes a hydraulic jump and the profile corresponding
to the flow computed for the enhanced rounding/beveling is supercritical,
then the end depth of the supercritical profile is taken as the full-flow-inducing
depth if it is larger than the end depth of the actual profile. If the
enhanced profile end depth is not larger, then TY5SBF is applied to define
the full-flow-inducing depth.
-
If the profile corresponding to the flow computed for the enhanced rounding/beveling
includes a hydraulic jump, and the actual profile includes a hydraulic
jump, and the actual jump is higher than the other jump, then type 5 flow
is rejected.
-
If the profile corresponding to the flow computed for the enhanced rounding/beveling
includes a hydraulic jump and the actual profile does not include a hydraulic
jump or includes a hydraulic jump too small to cause type 5 flow to be
rejected in step 7, the exit depth of the actual profile is varied above
critical depth until a hydraulic jump results, or the calculated hydraulic
jump is increased, to match the downstream depth of the jump in the profile
corresponding to the flow computed for the enhanced rounding/beveling.
This process extracts the maximum amount of information, perhaps more information
than is available, from figures 13 and 14.
The basis for these figures is not revealed in Bodhaine
(1968) or Carter (1957). Figures
13 and 14 are primarily based on laboratory
experiments done at the Georgia Institute of Technology by Jack Davidian.
In the laboratory, the transition between flow types 5 and 6, and between
flow types 1,2, or 3 and 5 or 6 could be accurately determined. Thus, the
figures and table available in Bodhaine (1968)
should be reasonably reliable in defining the boundaries between flow types
(Lamar Sanders, U.S. Geological Survey, written commun., 1995).
4.2.4 Transitions Between Flow Types
The development of tables of type 13 involves computation of 100 or
more distinct flow profiles. Some of these profiles will likely fall into
a transition region between culvert-flow types. As the water level at section
1 increases, the free flow will pass from one culvert-flow type to another
with some transition between them. Sometimes the transition is smooth,
and sometimes it is not. For example, a pipe culvert at small, upstream
head levels could be in culvert-flow type 2. As the upstream head increases,
the culvert-flow could become type 1. As the upstream head continues to
increase, the culvert-flow type could shift back to type 2 because the
converging side walls cause the critical flow to increase rapidly. Eventually,
the culvert-flow type could become type 5 or type 6, or both, depending
on the slope, length, and roughness of the culvert barrel. Some of the
computational transitions between flow types are reasonably smooth because
of the equations utilized. For example, the transition between types 1
and 2 is computationally smooth because of the nature of the governing
equations. Thus, no special treatment is implemented for this transition.
In the following discussion the concern is with the computed flows
and not the actual flows in the transition. The actual flow may be quite
unstable and oscillatory in some transitions, and an approach must be developed
in which these features of the actual flow are ignored but for which accurate
routing of flows through the culvert is obtained.
The approach taken for defining equations for the transitions is as
follows.
-
Limits for the various culvert-flow types are computed. The limit is the
water-surface elevation (upstream head) at section 1 at which the equation
for a given culvert-flow type no longer applies or is no longer permitted
to apply. For example, the limit for culvert-flow type 2 is defined as
the flow with a water level at section 2, computed ignoring flow-contraction
effects at the entrance but including the expansion losses downstream from
section 2, just in contact with the soffit of the culvert at the entrance.
The water-surface elevation at section 1 for this condition is then the
type 2 flow limit. If the water-surface elevation at section 1 is above
this limit, the flow is no longer type 2. The limits are summarized in
table 4. A natural limit for culvert-flow type 1 results from the geometry
of box culverts that is in a reasonable range. However, the converging
side walls in culverts of other shapes cause critical flow to increase
without bound as flow depth approaches the culvert soffit. Consequently,
a limit on culvert-flow type 1 controlled by the depth at section 2 may
result in a water-surface elevation at section 1 that is above the value
observed to normally induce full flow at the entrance to the culvert. The
default value of the maximum water-surface height at section 2 for culvert-flow
type 1, y 2max, is 0.95 D 2, and the
default value of the maximum water-surface elevation at section 1 for culvert-flow
type 1,
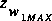 , is
, is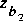 + 1.4 D 2 in FEQUTL computations. These defaults can
be overridden by optional user input in the CULVERT command. The input
parameters are TY1YTD and TY1HTD. Complete input details for these parameters
are provided in section 5.5. The upper
limits for culvert-flow types 1 and 2 are set lower than the lower limits
for culvert-flow types 5 and 6 to allow transitional flow to be computed.
+ 1.4 D 2 in FEQUTL computations. These defaults can
be overridden by optional user input in the CULVERT command. The input
parameters are TY1YTD and TY1HTD. Complete input details for these parameters
are provided in section 5.5. The upper
limits for culvert-flow types 1 and 2 are set lower than the lower limits
for culvert-flow types 5 and 6 to allow transitional flow to be computed.

-
The transitional flow types are utilized between the upper limits of the
low-head culvert-flow types (1 and 2) and the lower limits of the high-head
culvert-flow types (5 and 6). The equation for the high-head flow type is
forced to match the flow and downstream water-surface-elevation limit of
the low-head flow type. This is accomplished by computing a discharge coefficient
for culvert-flow type 6 or a contraction coefficient for culvert-flow type
5 that will match the flow for the corresponding low-head culvert-flow.
If this is not possible, no transition is computed and the user must adjust
the resulting function table of type 13 manually if one or more transitions
are too abrupt. The downstream water-surface-elevation limit is the tail-water
elevation at which free flow ends and submerged flow begins. For example,
for culvert-flow type 2, the downstream water-surface-elevation limit is
critical depth in the culvert barrel.
-
For any water-surface elevation at section 1 in a transition region, the
downstream condition and the discharge or contraction coefficient are varied
linearly with elevation at section 1 between the values at the lower and
upper limits of the transition region. For example, the upper limit for
a culvert flow of type 2 in a given culvert might be 8.4 ft with a critical
depth at the culvert exit (section 3) of 4.5 ft and a discharge coefficient
of 0.95. For this same culvert, the lower limit for a culvert-flow of type
6 might be 10.5 ft with a piezometric level at the culvert exit of 4.8
ft and a discharge coefficient of 0.84. Assuming that the discharge, upstream
water-surface elevation, and downstream (section 3) piezometric level corresponding
to the upper limit for culvert-flow type 2 are applied in
equation 85 describing culvert-flow type 6, the discharge coefficient
for culvert-flow type 6 would be 0.78. For an upstream water-surface elevation
of 9.45 ft, at the middle of the transition region, the discharge coefficient
for culvert-flow type 6 would be 0.81 and the piezometric level at the
culvert exit would be 4.65 ft. Physical realism is sacrificed for transitional
smoothness in this approximation. Both the piezometric level at the culvert
exit and the discharge coefficient may be physically unrealistic or unattainable
in any real flow. Such unrealistic conditions are not important in model
simulation; the transitional flow that results in the physical system cannot
be computed because it is physically unstable. All that is required for
computational accuracy is that the transitional flows be in a reasonable
range. Flow types 51, 52, and 62 are the corresponding transitional types.
-
Culvert flow type 61 is transitional and may be stable. At its upper limit,
the discharge coefficient is taken as if the culvert-flow were type 6.
Its lower limit is the upper limit of culvert-flow type 2. Critical flow
results at the culvert exit for both culvert-flow types 2 and 61. Thus,
only the discharge coefficient is varied between the lower limit and upper
limit of culvert-flow type 61. The transition between culvert-flow types
61 and 6 is treated the same as in item 3 with culvert-flow type 61 defining
the conditions that the equation describing culvert-flow type 6 (equation
85) must match.
Transitions between free-flow types and submerged flow types as well as
between submerged flow types must be considered. Some transitions, such
as between culvert-flow types 6 and 4 are smooth, as long as culvert-flow
type 42 is recognized. The transition between culvert-flow types 3 and
4 can be abrupt. However, considerable uncertainty results regarding the
details of the transition from part-full flow to full flow for the culvert.
Thus, the transition from culvert-flow type 3 to culvert-flow type 4 is
usually accomplished through culvert-flow type 41. The conditions that
cause the barrel to flow full are not explicitly determined. Whether the
barrel is flowing full is determined by the water level at section 43.
The transition from culvert-flow type 3 to type 4 is smoothed with culvert-flow
type 41 without an explicit identification of the transition.
The transition from free-flow, culvert-flow type 5 to full-pipe flow
is not smooth. Culvert-flow type 5 is unstable in that adequate ventilation
of the free space above the water in the barrel must be available. When
this ventilation is restricted by the friction of the air flow in the barrel
or by a hydraulic jump in the barrel or at the exit of the barrel, the
barrel will abruptly switch from part-full flow to full flow. This transition
is marked by an increase in the flow as the barrel is used more efficiently.
This change in discharge can be 30 percent or more. This transition is
unstable because the increase in discharge may induce air entrainment at
the entrance through one or more vortices. The entrainment of this air
may allow the flow to momentarily be part full. Thus, the flow surges and
oscillates until the upstream water-surface elevation rises enough to prevent
substantial entrainment of air at the culvert entrance. During this time,
the value for flow in the culvert is probably between the culvert-flow
type 5 value and the value when the barrel is flowing full throughout (culvert-flow
type 4). Therefore, a special discharge coefficient for the equation describing
culvert-flow type 5 is computed in the CULVERT command such that the culvert-flow
type 4 matches the culvert-flow type 5 at its limit. This coefficient is
then varied linearly between the culvert-flow type 5 submergence (full-flow
inducing) level and the current downstream water-surface elevation. This
interpolation continues until the current downstream water-surface elevation
is at or above the exit soffit. Then the culvert-flow becomes type 4. The
transitional culvert flow is denoted 42 because it is full flow and the
piezometric level at the culvert exit is below the culvert soffit.
4.2.5 Departure-Reach Losses
Update available for flapgate
losses
Bodhaine (1968) took the departure
reach losses to equal complete loss of the velocity-head difference between
the culvert exit and the departure section. In general, this loss is too
large. The cumulative effect of using this simple loss on a sequence of
culverts along a stream in an urban area could substantially bias the computed
water-surface elevations. Therefore, a simple momentum balance in the departure
reach is applied in FEQUTL following
Henderson (1966, p. 208-210). This approach or variations have been
applied and described by Schneider
and others (1977).
In Bodhaine (1968), the losses
at the exit of the culvert are estimated using the complete loss of velocity-head
difference between the exit of the culvert, section 3, and the departure
reach, section 4. This would seem to imply that this loss method must be
used for consistency in the selection and application of discharge coefficients.
However, this implication is incorrect as described in the following discussion.
Culvert-flow types 3 and 4 in Bodhaine
(1968) are the only flow types that can be affected by exit losses.
The other culvert-flow types are free of tail-water effects by definition
and, therefore, the discharge coefficients are independent of any assumptions
made about the losses in the departure reach. The only effect of exit-loss
assumptions on culvert-flow types 1, 2, 5, and 6 involve the conditions
that must be present at section 4 for these flow types to be valid.
The discharge coefficients for culvert-flow types 4 and 6 are identical
in Bodhaine (1968). These culvert-flow
types only differ in the conditions in the departure reach, with the exit
of the culvert submerged in type 4 flow so that tail water affects the
flow. Bodhaine (1968) points out
that the piezometric level at section 3 is below the soffit of the culvert,
but no statement is given on submergence-level effects below the soffit.
In FEQUTL, additional culvert-flow types have been included in the CULVERT
command to represent submergence of type 6 flow when the tail water is
above the exit piezometric level but below the soffit. The deviation of
the discharge coefficient from the ideal value of unity for these flow
types is a reflection of the energy losses incurred at the contraction
and expansion of the flow near the culvert entrance. These contraction
and expansion effects are identical in both culvert-flow types 4 and 6.
Consequently, the assumptions regarding the exit losses cannot have a significant
effect on the model experiments that yielded the discharge coefficients
for culvert-flow type 4. Otherwise, the computed discharge coefficients
would have differed significantly from those found for culvert-flow type
6. Therefore, in both culvert-flow types 6 and 4, the piezometric level
at the exit is the proper value for computing the flows with the discharge
coefficients. The only difference is that for culvert-flow types 6 and
4, the piezometric level is below the water surface and at the water surface,
respectively.
Culvert-flow type 3 is similar to culvert-flow types 1 and 2 except
that tail water affects the type 3 flow. However,
Bodhaine (1968) gives the discharge coefficients for all three flow
types using the same relation. Bodhaine
(1968) gives the base discharge coefficient for pipe culverts in figures
20 and 25 and the discharge coefficient for box culverts in figure 23.
Culvert-flow types 1 and 2 are independent of the treatment of losses in
the departure reach. Again, if the culvert-flow type 3 discharge coefficients
in the model experiments were greatly affected by the treatment of the
departure reach losses, it seems unreasonable to expect that the discharge
coefficients would follow the same relation. Therefore, the proper value
of the water-surface elevation for culvert-flow type 3 is the water-surface
elevation at section 3.
The unpublished details and raw results of the laboratory model study
utilized to develop Bodhaine (1968)
have been lost since the experiments were completed about 40 years ago.
Therefore, the sizes of the model approach section and departure section
relative to the model culvert barrel is unknown. Nevertheless, considering
the goal of the study, peak-flow estimation, and the need to reduce computational
effort, it seems logical that the model would have a departure reach much
larger in flow area than the area of the culvert barrel. In this case,
the water-surface elevation at section 3 approaches that at section 4 as
shown by a simple momentum balance. The equivalence of water-surface elevations
in sections 3 and 4 is a close approximation of the conditions most likely
to be found in the field in natural channels at flood stage. If the departure-reach
flow area is large enough relative to culvert flow area, then the assumption
of an exit loss given by the difference in velocity heads is valid. It
is reasonable to assume that the model departure reach was sized so that
this was the case. This avoids the tedious calculations of the momentum
balance in the departure reach before the common availability of digital
computers.
In summary, the application of the momentum balance for the departure
reach losses is consistent with the discharge coefficients in Bodhaine
(1968), and it results in more reasonable losses for culvert-departure
conditions that violate the assumptions implicit in application of the
difference in velocity heads as the estimate of the energy loss in the
departure reach. Assumption of complete loss of the difference in velocity
heads in the culvert departure reach often results in an overestimation
of the losses and, in some cases, a gross overestimation of the losses.
The simple momentum balance provides a reasonable alternative that maintains
basic validity to the limit of a departure reach with the same width as
the culvert exit. In that limit, the simple momentum balance gives results
for a submerged hydraulic jump in a rectangular channel. Assuming complete
loss of the velocity-head difference can lead to an underestimate of the
culvert discharge when the departure reach has a flow area only a few times
larger than the culvert exit. This underestimation is corrected by using
a simple momentum balance to estimate the conditions at section 3 from
the conditions at section 4.
In applying a simple momentum balance, it is assumed that the departure
reach is horizontal, prismatic, and frictionless. The simple momentum balance
is calculated for sections 3, 43, 44, and 4 shown in figure 3. Section
43, the cross section of the stream channel a short distance downstream
from the culvert exit, represents the upstream end of the control volume
for the simple momentum balance. Section 44 represents the downstream end
of the control volume for the simple momentum balance. The distance between
these two sections is not considered in the computations because friction
and bottom slope are ignored. The geometry of section 44 is always the
same as section 43 because a prismatic channel is assumed in the simple
momentum balance. Different designations are applied because the water-surface
elevation and water-surface height in these sections will differ. If the
departure reach is prismatic and horizontal, the geometry of section 4
will be the same as sections 44 and 43 with the same water-surface elevation
as section 44.
If the departure reach is not horizontal or prismatic, then the geometry
of section 4 will differ from section 43. However, section 44 will still
be the same as section 43, defining a horizontal and prismatic subreach
in the departure reach. This is needed for the simple momentum balance.
A simple momentum balance is used to estimate the losses in this case because
the application of the momentum balance to a nonhorizontal or nonprismatic
control volume requires knowledge of the water-surface profile in the control
volume. Simple assumptions regarding this profile may introduce errors
so large that the results become useless. This is analogous to the representation
of a hydraulic jump. A simple momentum balance produces a close match to
measurements if the jump is in a prismatic, nearly horizontal channel.
If the channel is nonprismatic or nonhorizontal, simple estimation of the
gravity force or of the downstream component of the pressure forces on
the sides of the channel fails to produce good results, and laboratory
measurements must be made. No such measurements are available for the departure
reaches of culverts, and only a limited number of measurements are available
for hydraulic jumps.
The simple energy balance between sections 44 and 4 is
(90)
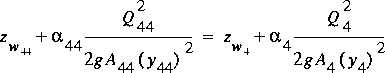 ,
,
where Q 44 = Q 4 = Q B
+Q r . The water-surface elevation at section 4 is transferred
to section 44 by applying equation 90 and assuming no energy losses. The
assumption of no energy loss resulting from friction is reasonable because
of the short distance between sections 44 and 4. The simple momentum balance
becomes
(91)
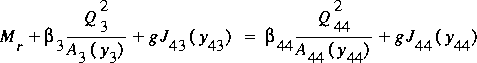 .
.
Equations 90 and 91 give the relations for the departure reach once
the culvert and roadway flows and momentum fluxes are known.
4.2.6 Outline of Solution Process for Culvert Flow
The solution process for culvert-flow proceeds in the following major
steps for each upstream head given by the user. The datum for head is the
maximum value of the elevations of the minimum points at sections 1-4.
-
The free flow over the roadway, if any, is determined. The drop to free
flow for the flow over the roadway (that is, the difference in elevation
between the water surface at sections 1 and 43 at incipient submergence
of the free flow) also is computed in this step.
-
The free flow and the flow type for the culvert are determined. All free-flow
type transitions are included in this step as is the computation of the
free-flow limits.
-
The departure reach for the free flow is computed. The conditions at section
3 and section 43 are known. The flow and momentum flux for the roadway
are known. Equation 91 is solved
for the water-surface height and, therefore, the elevation at section 44.
Equation 90 is then solved for the
water-surface height at section 4. The drop to free flow for the 2-D table
is then given by the difference in water-surface elevations between sections
1 and 4. A case may result where no solution is possible. This indicates
the control is at section 4, and the free-flow type is type 7. Free drop
and the free flow must be computed at a later step (see step 9).
-
The drop between the water-surface elevation at section 1 and the piezometric
level at section 3 corresponding to the free flow determined in step 2
is computed. A series of tail-water elevations at section 43 is computed
covering the range from the minimum, the free-flow piezometric level, to
the maximum, the water-surface elevation at section 1. The distribution
of partial drops specified by the user defines the series of downstream
water-surface elevations to be evaluated in the CULVERT command. The drop
from section 1 to section 43 must be distinguished from the drop from section
1 to section 4.
-
The flow in the culvert and the flow over the roadway are computed for
each downstream water-surface elevation determined in step 4 above the
minimum elevation for free flow. The flow in the culvert will be submerged.
The water-surface elevations at sections 1 and 43 are known, so the only
unknown is the flow in the culvert. The flow over the roadway is computed
first because it can affect the flow in the culvert through the velocity
head at section 1. The square root of the drop in water-surface elevation
from section 1 to section 43 is then computed.
-
A function relating the sequence of culvert-flows and the associated square
root of drop is determined. A variation-limited cubic spline is fitted to
these values with flow taken as a function of square root of drop. The
points defining the fit are called knots. Thus, the knots in this case
are the values of square root of drop at which the culvert-flow was computed.
An interior knot is any knot that is not at the beginning or end of the
sequence of knots. A cubic spline is a piecewise cubic polynomial with
the function value, first derivative, and second derivative being continuous
at each interior knot. A variation-limited cubic spline is a cubic spline
in which the variation of the spline between adjacent knots is monotonic;
that is, the first derivative always has the same sign. The purpose of
requiring that the first derivative be monotonic is to prevent introducing
new extreme values by interpolation between knots. If this is not done,
the fit of the cubic spline or other nonlinear function could result in
new extremes that are invalid. Because the spline is variation limited,
extreme values not already present at the knots will not be produced by
interpolation. In some cases, the spline is not variation limited. The
computed first derivatives at the knots are then adjusted in FEQUTL to
force the piecewise cubic polynomial to have monotonic variation. This
no longer results in a cubic spline because the adjustment of the first
derivative causes the second derivative at the adjusted knot to be discontinuous.
However, the simulated model fit to the data may still be excellent. Once
the function is defined, it is stored in a function table for later use.
-
A function that gives the flow-defining area at the culvert exit as a function
of the water-surface elevation at section 43 is determined. The culvert
can be flowing full or part full. The function will have a unique value
for each water-surface elevation at section 43 for a given upstream water-surface
elevation. A piecewise linear function is adequate to define the water-surface
elevation at the culvert exit. This function is stored in a function table
of type 2 for later use. If the water-surface elevation at the culvert
exit is known, the flow area can be computed for the culvert exit. If the
flow area and the flow are known, the momentum flux for the flow at the
culvert exit can be computed.
-
The flow and the momentum flux over the road are easily computed as needed,
so special tables are not used. These values are always computed from basic
definitions. This is efficient because submergence of flows over embankment-shaped
weirs is affected by downstream water-surface elevation only when that
elevation is higher than about 70 percent or more of the approach head.
Usually, the flows computed for the last few downstream water-surface elevations
as the upstream water-surface elevation is approached deviate from the
free-flow values.
-
If the freeflow corresponds to culvert-flow type 7, the free flow and the
drop to free flow are calculated. Culvert-flow type 7 is a submerged flow
in the culvert because the control at section 4 drowns all other controls.
The following steps are applied to calculate the free flow and drop to
free flow.
- 1.
A water-surface height at section 43, y 43, is selected.
This water-surface height defines the flow in the culvert with the associated
momentum flux by using the special tables developed in steps 6 and 7. The
flow and momentum flux over the roadway are computed. The water-surface
height, y 43, defines all cross-sectional characteristics
needed at section 43.
- 2.
The flows are now known, so critical water-surface height at section 4
may be computed. This defines all other values at section 4. Equation
90 is solved for the flow and water-surface height at section 44. This
defines all cross-sectional characteristics needed at section 44.
- 3.
Flow and water-surface-height values at section 43 and section 44 are defined.
These values are applied in equation
91 to compute the left-hand side and the right-hand side of the equation.
If the two sides are in close agreement, the solution for free flow is
found. If not, a new depth is selected at section 43 that will improve
the agreement and steps 9.1-9.3 are repeated.
-
The partial free drops between sections 1 and 4 are computed. These are
not the same as the drops between sections 1 and 43. From these drops the
corresponding water-surface elevations at section 4 are computed, starting
at the minimum elevation at free flow and ending at an elevation equal
to the elevation at section 1.
-
For each elevation computed in item 10, the submerged flow is determined
utilizing the departure-reach equations, 90 and 91. The process is as follows.
- 1.
A water-surface height at section 43, y 43, is selected.
This water-surface height defines the flow in the culvert with the associated
momentum flux by utilizing the special tables developed in steps 6 and
7. The flow and momentum flux over the roadway are computed. The water-surface
height, y 43, defines all cross-sectional characteristics
needed at section 43.
- 2.
The flows are now known, so flow and water-surface-height values at section
4 are known. Equation 90 is solved for the flow and water-surface-height
values at section 44. This defines all cross-sectional characteristics
needed at section 44.
- 3.
Flow and water-surface height-values at section 43 and section 44 are defined.
These values are applied in equation
91. If the two sides of equation
91 are in close agreement, the solution for flow and water-surface
height is found. If not, a new water-surface height is selected at section
43 that will improve the agreement and steps 11.1-11.3 are repeated.
4.2.7 Momentum Flux for Flow Over the Roadway
The momentum flux over the roadway enters into the simple momentum
balance for the departure reach. It is assumed that the horizontal momentum
flux over the roadway enters the channel unaffected by gravitational acceleration
or flow resistance down the roadway embankment. When the flow over the
roadway becomes a large part of the total flow, the momentum flux must
be considered. For moderate depths of flow over a roadway, the depth is
approximately critical depth when the flow is free of downstream effects.
Assuming that the flow over the roadway is critical results in the depth
as
(92)
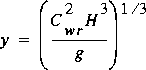 ,
,
where C wr is the weir coefficient and H is
the head on the roadway (depth of flow relative to the minimum point on
the roadway embankment) utilized to compute the weir flow. The estimated
momentum flux per unit width of roadway, q r 2
/ y, becomes
(93)
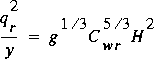 ,
,
where q r is the flow per unit width of roadway. The
weir coefficient includes the effects of friction losses in the approach
and other factors. The flux per unit width is integrated along the roadway
crest as the flow per unit width. Additional details are provided in
section 4.3.
When the flow over the roadway is submerged, equations 92 and 93 are
not valid. The flow is no longer approximately critical, and the flow is
reduced from that given by the unit-width weir equation (equation 93).
The crest depth for submerged flow is estimated in FEQUTL assuming that
the loss of energy from section 1 to the roadway crest will be in the same
proportion to the loss of energy from section 1 to section 43 as for incipient
submergence. In equation form this assumption becomes
(94)
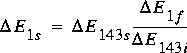 ,
,
where
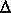 E 1 s is the energy
loss from section 1 to the roadway crest when the flow over the roadway
is
submerged;
E 1 s is the energy
loss from section 1 to the roadway crest when the flow over the roadway
is
submerged;
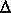 E 143 s is the energy
loss from section 1 and 43 when the flow over the roadway is submerged;
E 143 s is the energy
loss from section 1 and 43 when the flow over the roadway is submerged;
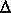 E 1 f is the energy
loss from section 1 to the roadway crest when the flow over the roadway
is
free; and
E 1 f is the energy
loss from section 1 to the roadway crest when the flow over the roadway
is
free; and
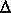 E 143 i is the energy
loss from section 1 to section 43 at incipient submergence of the free
flow.
E 143 i is the energy
loss from section 1 to section 43 at incipient submergence of the free
flow.
The loss ratio at incipient submergence is assumed to remain the
same for submerged conditions in FEQUTL computations. The specific energy
at the roadway crest for submerged flow is computed and inverted to find
the crest depth for submerged flow. This crest depth is then used to estimate
the momentum flux for submerged flow.
Assuming critical flow on the crest, the energy loss from section 1
to the roadway crest at free flow is
(95)
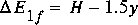 .
.
Assuming that the roadway embankment height, P e,
above the approach reach is about the same as its height above the departure
reach, the loss from section 1 to section 4 at incipient submergence is
estimated from
(96)
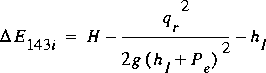 ,
,
where h I is the piezometric downstream head at incipient
submergence measured from the roadway crest. The energy loss from section
1 to section 43,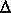 E 143 s,
is given by equation 96 with h I, the downstream head
at incipient submergence, replaced by h t, the downstream
head causing submergence.
E 143 s,
is given by equation 96 with h I, the downstream head
at incipient submergence, replaced by h t, the downstream
head causing submergence.
Several checks on the results for the submerged crest depth are performed
in FEQUTL computations. The loss ratio is given a minimum value of 0.005.
Also, the crest depth computed for submerged flow is not permitted to be
less than the crest depth for free flow at the given upstream head.
The momentum flux over the roadway crest may not be a good estimate
of the effective flux that enters the control volume of the departure reach
for the simple momentum balance. The pathway of flow over the roadway entering
the departure reach should be considered. Many rural and suburban roads
do not have curbs and gutters. Ditches adjacent to the roadway serve as
drainage channels. A portion of the water flowing over a roadway at a culvert
crossing may be intercepted by the ditch on the downstream side of the
road. This water is then delivered to the departure reach of the culvert.
This water enters the departure reach at approximately a right angle. Therefore,
the effective momentum flux in the downstream direction from the flow over
the roadway is much smaller than the momentum flux computed for the flow
over the roadway. A fixed factor is included in FEQUTL as a multiplier
on the estimated momentum flux over the roadway to better estimate the
effective flux for the simple momentum balance used in the departure reach.
4.2.8 Special Losses
Culverts commonly are placed in a stream in a manner that departs markedly
from the placement assumed in the laboratory tests on which the loss estimates
are based. For example, for reasons of simplicity, economy, or physical
restrictions, culverts commonly are placed so that the stream approaches
the culvert perpendicular to the barrel and makes a sharp right-angled
bend immediately upstream from the culvert entrance. An input value, APPLOS,
is included in FEQUTL and is taken as a factor on the approach velocity
head to represent additional losses. When the flow entering the culvert
undergoes an expansion, the loss coefficients determined in laboratory
tests do not apply. The input value, APPEXP, is then applied as a factor
on the velocity-head difference between sections 1 and 2.
4.2.9 Summary of the CULVERT Command
This discussion of the CULVERT command contains a simplified outline
of the steps in the solution process. Many special conditions must be detected
and addressed. One of the more difficult problems is convergence failure
at some point in the solution process. The process has many iterative solutions:
steady-flow profiles, critical depth, normal depth, inversion of specific
energy, inversion of specific force, and others. A failure to converge
could arise from a user error, a program error, or an incorrectly selected
path. Tests are included in the program code to distinguish these causes
of convergence failure, but sometimes these causes cannot be determined
in the tests. Only a subset of all possible culverts can be computed with
the CULVERT command.
Two common cases result in computational failure in the CULVERT command.
One case where problems arise is in computation of culvert-flow type 0.
This flow type only should result at low flows when the culvert barrel
has a greater capacity than does the low-flow channel in the approach section.
No transitions for type 0 flow are provided in FEQUTL. If type 0 flow results
for moderate to high flows, it is likely that the approach section is invalid.
A related condition arises with flow over the road. All the flow in
the culvert and over the roadway must pass through the approach section.
If the length of overflow for the roadway is too wide, culvert-flow type
0 will result. Critical control at section 1 is assumed in culvert-flow
type 0. For computation of flow over the roadway it is assumed that critical
control cannot result at section 1. These two assumptions conflict, and
computational failure or problems will result. The flow over the roadway
is computed, if possible, as long as the flow is less than or equal to
the critical flow in section 1. This is done only to provide a result that
can be interpreted. Flow over the road and culvert-flow type 0 are not
compatible. If culvert-flow type 0 results at moderate to high flows or
with flow over the road, then the representation of the culvert must be
changed. Two alternative representations of the culvert are possible.
The flow over the road can be computed separately from the flow in the
culvert by applying the EMBANKQ command (section
5.6). Calculation of the flow over the road with the CULVERT command
is suppressed by specifying a high value for the elevation of the roadway
crest. Two flow tables will be computed in FEQUTL: one for flow over the
road and the other for flow through the culvert barrel. These flow tables
are then used in parallel in FEQ to represent the culvert. Some of the
interaction between the two flow paths is lost. However, this may be applied
if the flow over the road is at a distance from the culvert or if the flow
over the road is large relative to the flow through the culvert.
The other alternative for computing flow over the road and through the
culvert is introduction of an explicit expansion upstream from the culvert
applying the EXPCON command (section 5.7).
The approach section, which is smaller than the culvert opening, is utilized
as the upstream cross section for the expansion. A new approach section,
made large enough that the flow always contracts as it enters the culvert,
is then utilized for the approach section for the culvert and as the downstream
section for the expansion. In the FEQ model, the expansion is connected
to the culvert with a short branch, usually only 1 or 2 ft long, with the
new approach section of the culvert defining the cross section for the
branch.
Neither of these alternatives account for the lack of knowledge of the
physics of flows expanding at a culvert. However, these alternatives account
for the problem of computational failure. Only a careful field check of
the cross sections can reveal if they are properly measured. Unless the
culvert opening is partially blocked, a cross section must be available
that is larger than the culvert opening. If the culvert opening is partially
blocked, then the barrel cross section utilized is incorrect.
- 4.2.1 Additional Flow Types
- 4.2.2 General Routing Methodology for Culvert Flow
- 4.2.3 Routing Methodology for Culvert-Flow Type 5
- 4.2.4 Transitions Between Flow Types
- 4.2.5 Departure-Reach Losses
- 4.2.6 Outline of Solution Process for Culvert Flow
- 4.2.7 Momentum Flux for Flow Over the Roadway
- 4.2.8 Special Losses
- 4.2.9 Summary of the CULVERT Command
[Next Section][Previous
Section] [Table of Contents]
 1.5 may be used because computations have shown
that, where submergence was uncertain, greater accuracy can be obtained
by assuming that the entrance is not submerged (low-head flow). However,
for routing of unsteady flow through the culvert, a more explicit consideration
of the transition region is necessary. As a specific example, Bodhaine
(1968, p.47) noted that, for a range of approach water-surface elevations,
the designation of the flow as low head (flow type 1) or high head (flow
type 5) is unstable. Laboratory data indicate that the unstable condition
begins at (zw1-zci)/ D = 1.2, where
the flow is usually low head, and ends at (zw1-zci)/
D = 1.5, where the flow usually becomes high head. Bodhaine
(1968) recommended that the culvert discharge rating in this range
of approach water-surface elevations between flow types 1 and 5 be represented
by a straight line between the discharge computed with low-head methods
at a ratio of 1.2 and the discharge computed with high-head methods at
a ratio of 1.5.
1.5 may be used because computations have shown
that, where submergence was uncertain, greater accuracy can be obtained
by assuming that the entrance is not submerged (low-head flow). However,
for routing of unsteady flow through the culvert, a more explicit consideration
of the transition region is necessary. As a specific example, Bodhaine
(1968, p.47) noted that, for a range of approach water-surface elevations,
the designation of the flow as low head (flow type 1) or high head (flow
type 5) is unstable. Laboratory data indicate that the unstable condition
begins at (zw1-zci)/ D = 1.2, where
the flow is usually low head, and ends at (zw1-zci)/
D = 1.5, where the flow usually becomes high head. Bodhaine
(1968) recommended that the culvert discharge rating in this range
of approach water-surface elevations between flow types 1 and 5 be represented
by a straight line between the discharge computed with low-head methods
at a ratio of 1.2 and the discharge computed with high-head methods at
a ratio of 1.5.
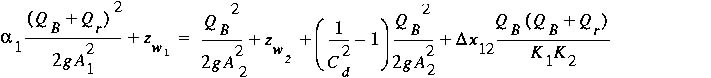
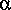 1
1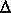 x 12
x 12 ,
, ,
,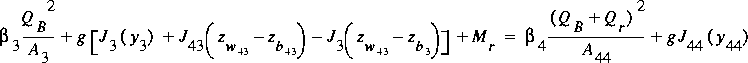 ,
,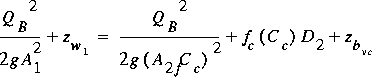 ,
,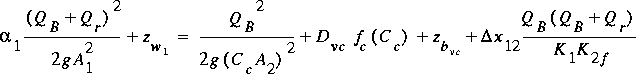 ,
,
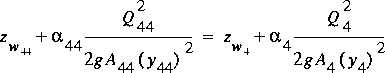 ,
,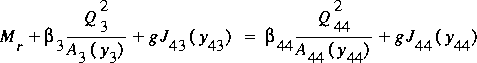 .
.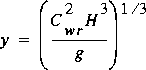 ,
,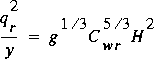 ,
,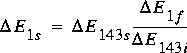 ,
,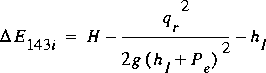 ,
,