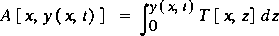,
Full Equations (FEQ) Model for the Solution of the Full, Dynamic Equations of Motion for One-Dimensional Unsteady Flow in Open Channels and Through
Control Structures
(6)
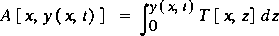,where z is height above the thalweg. The integrand, T[x,z], varies only with the height, z, from the minimum point in the cross section because the location along the channel, x, and the time, t, are held constant during the integration.
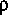g{y(x,t)-z}T[x,z]
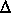z, where g is the acceleration of gravity. Thus, the pressure force, FP, on the cross section below y is given by the integration of the pressure forces on many small horizontal strips as(7)
.
Dividing equation 7 by 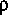g gives the first moment of area about the water surface as
(8)
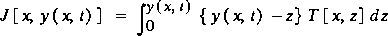.Expansion of equation 8 and integration by parts yields
(9)
,as a simpler relation for the first moment of area. The qualifier that the first moment should be about the water surface is now dropped, because this is the only axis where moments are determined.
The directional aspect of the hydrostatic pressure force has been ignored in keeping with the previous discussion. If direction were to be included, the cosine of the angle between the normal to the cross-section surface and the x-axis would have to be included in equations 7-9. However, the effect of omitting the direction is reduced to negligible levels with the cosine function, as was the result for the computation of the mass flux through a cross section in the flow.
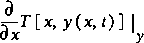
indicates that the height, y, is held constant and that the time variable is suppressed. This does not mean that time is held constant; on the contrary, time is ignored and the top-width function is defined by the distance along the channel, x, and the height above the minimum point, y. A shorthand form for this notation is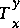 
, where the subscript denotes the variable used in taking the derivative and the superscript denotes the variable held constant. On the other hand,
indicates that only t is held constant. The height, y, can vary so long as the time is held constant.
The derivatives of area and first moment of area with respect to the water surface with distance along the channel may be determined by application of the Leibniz rule, resulting in
(10)
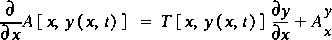
and
(11)
.
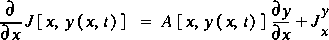The terms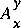 
and 
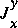are not needed if the channel is prismatic. The last term in equation 11, 
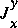, is related to the downstream component of the pressure force on the sides of the channel, which is given by the product of 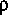g and the derivative of the first moment of area at constant depth with respect to distance along the channel, that is 
.
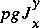The effects of the curvature of the cross section and the flow in the channel are ignored in these derivatives. Addition of the directional effect substantially increases the complexity of the analysis.
(12)
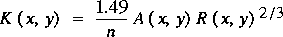,where R(x,y) is the hydraulic radius, which equals A(x,y)/P(x,y); and n is Manning's roughness coefficient. If the cross section is noncompact, it must be subdivided. The subdivision of compound and composite cross sections is discussed in Franz and Melching, 1997).
The average velocity is defined so that continuity is preserved. That is, the flow rate Q for the cross section is defined by
(13)
,
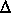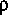where v is the velocity at each point in the cross section. The average velocity is then simply defined as V = Q/A. The momentum flux through a small area, A, is v2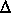A. The sum of these fluxes for the cross section becomes
(14)
.
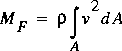For ease of computation, the momentum flux computed by use of the average velocity should be the same as the momentum flux computed from the point velocities in the cross section. Thus, a coefficient, 
, is introduced to correct for the errors resulting from use of the average velocity instead of the local-velocity field in the cross section. The defining equation for, , the momentum-flux correction coefficient, is then
(15)
,
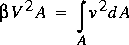where 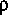is assumed to be constant and therefore is deleted from the relation. Solving for yields
(16)
.
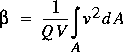The kinetic-energy-flux correction coefficient,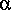 
, is defined in a similar manner. Kinetic energy replaces momentum in the concept development, and the defining equation is
(17)
,
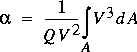where again 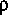is deleted.
For the case where the velocities are unidirectional (all downstream) but nonuniform across the section, Jaeger (1956, p. 115) found that
,
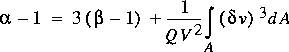where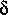 
v = v - V and is the deviation of the point velocity from the average velocity. Equations 16 and 17 indicate that 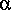is greater than .
Stream analyses have provided considerable evidence that values of 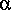and are significantly and frequently different from 1. For example, 36 of 62 values of computed by the U.S. Geological Survey from current-meter measurements [NOTE2] were substantially greater than 1 for natural trapezoidal-shaped channels without overbank flow, bridge piers, or other manmade obstructions. Thus, these channels were compact, yet was greater than 1.1 in more than one-half of the channels; in fact, was greater than 1.2 for 8 of the 62 channel measurements. Further, 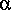was greater than 1.3 and greater than 1.5 in 30 and 13 channel measurements, respectively. The average value of 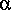for the 62 measurements was 1.36, and the average for was 1.12. These measurements show that the flux correction coefficients may be substantially different from 1 in compact natural channels. Consideration of extensive overbank flow could make the values of a and b much higher. Therefore, the effect of velocity distribution may have to be included in the governing equations.
Recent research by Xia and Yen (1994) indicates that the effects of flow nonuniformity and of approximations of may not substantially affect the calculated water-surface profile. Xia and Yen (1994) compared the relative accuracy of the Saint-Venant equations ( = 1) with the results from the nearly exact momentum equations (Yen, 1973), including pressure correction coefficients (k and k') and not equal to 1. A series of numerical experiments was done for various values of k, k', and (parameter interaction was only partially considered) for flow subject to various downstream backwater conditions. These experiments involved routing a sinusoidal stage hydrograph with a peak 2.25 times the base stage,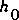 
, through a 54-mile long channel of rectangular, wide rectangular, or trapezoidal geometry. The maximum error in the computed depth was found to be 0.36 percent for = 1.33 and 1.11 percent for = 2 for a channel with a bed slope of 0.00019 and downstream backwater ranging from 0 to 2.53 times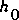 
. Thus, a reasonable approximation of should not result in substantial error in the computed water-surface profile.
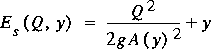.(Explicit functional notation is applied in equation 19 to emphasize dependence on water-surface height and flow rate. Subsequent equations will include explicit arguments only when necessary to show the functional dependence. Otherwise, any cross-sectional characteristic in an equation is a function of the water-surface height in the cross section.) If the partial derivative of specific energy with respect to water-surface height is set to zero, the result is
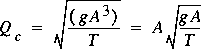,for the critical flow. Here, Qc is the critical flow rate producing a minimum in the specific energy at a given water-surface height, y. Hereafter, for convenience, critical flow is the basis for discussion rather than the water-surface height at critical flow. Most introductory treatments of critical flow go on to develop the concept of force plus momentum, M, called specific force by Chow (1959, p. 53). Specific force is the sum of the hydrostatic pressure force on a cross section and the momentum flux for the section (treating the density of water as 1 because it is constant). Thus, specific force is defined as
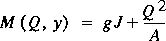.If the partial derivative of specific force with respect to water-surface height is set equal to zero, the result is
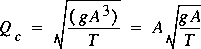,which is the same as the result obtained from minimization of specific energy.
Much is made of the equivalence of critical flow defined from specific momentum and specific energy in some introductory hydraulics texts and with good reason. If the cross sections are compact and the velocity distribution is virtually uniform, then equivalence of critical flow determined from specific energy and specific force follows. However, when the flow is sufficiently nonuniform to require values of > 1 and > 1 be included in the analysis, mathematical inconsistencies can arise for steady, gradually varied, nonuniform flow. In most discussions, the effects of nonuniformity are not considered, and the inconsistencies resulting from not equal to not equal to 1 are not recognized.
Generalizing the specific energy and the specific force values to include the flux-correction coefficients yields
and
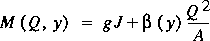.As indicated in equations 23 and 24, the flux coefficients vary with the water-surface height in the cross section (Chow, 1959, p. 43). Again, if the partial derivatives with respect to water-surface height are set to zero and the equations are solved for the critical flow, the result is
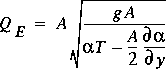
and
,
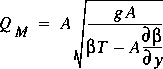where QE is the critical flow defined from specific energy and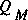 
is the critical flow defined from specific force. These results clearly show that the functions representing the flux-correction coefficients must follow certain restrictions for these two values to be the same at all depths.
Jaeger (1956, p. 93-119) extensively discusses the equivalence of these two definitions of critical flow. He includes coefficients for potential energy and hydrostatic-pressure force to correct for the effect of streamline curvature and he is able to show that the two values of critical flow are the same. This equivalence is based on the assumption that the appropriate correction-coefficient values have been used. In the above derivation, substantial inconsistency may result for some flows if only the flux-correction coefficients are applied. Experiments with steady uniform flow in a laboratory compound channel with flood plains indicate that minimization of specific energy or minimization of specific force yielded the same values for critical flow and water-surface height (Blalock and Sturm, 1981, 1983). In these experiments, many point measurements of velocity were made to accurately estimate the values of 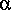and . If the flux-correction coefficients are included in the analysis and if they are estimated by the usual means (applying subsection conveyances as a surrogate for the velocity distribution), then the difference in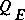 
and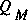 
can be greater than 30 percent. It should be recognized immediately that the flux-correction coefficients cannot be computed exactly because the calculated velocity distribution is only approximate. Thus, part of the large differences in 
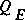and 
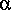reflects the approximate values of and .
Direct observation of critical flow in a stream is impossible. Thus, inferences about flow values must be made from the mathematical description of the flow. Consequently, the value computed for critical flow will depend on the governing equation selected to describe the flow. A change in the choice of the governing equation or in the terms to be included in such an equation will change the computed value of critical flow. Furthermore, critical flow results in mathematical problems (singularities) in the governing equations, such as division of a quantity by zero. These singularities are commonly a direct result of ignoring certain terms in the governing equations. The classic example is the flow of water over a brink. The 1-D governing equations indicate that the water-surface slope at the brink should be vertical and the depth should be the critical depth; however, as the flow approaches the brink, the streamlines become strongly curved and the pressure distribution deviates appreciably from hydrostatic. This deviation violates the assumption of the governing equation. Thus, the depth at the brink is not the critical depth nor is the water surface vertical. The critical depth as computed from equation 20 is some distance upstream from the brink, and the depth at the brink is appreciably less than the critical depth given by equation 20 (Henderson, 1966, p. 191).
Steady flow has been assumed in equations 19-26. Blalock and Sturm (1983), however, show that equations 25 and 26 also are obtained from unsteady-flow governing equations. These equations include the effect of velocity distribution, but deviations from hydrostatic pressure distribution are ignored; these are the typical assumptions made in current applications of steady and unsteady flow. The unsteady-flow governing equations applied by Blalock and Sturm (1983) are of the same form as those developed in section 5.
Although the equations for critical flow derived from steady and unsteady flow are the same, the velocity distribution in a channel at a given stage may not be the same for steady flow as for unsteady flow. The difference could be substantial in a compound channel. If the stage is rising, water will be moving from the main channel into the flood plains; whereas if the stage is falling, the water will move in the opposite direction. This flow interchange with the flood plains must have an effect on the velocity distribution and, therefore, on 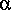and . This interchange also indicates that the simple assumption that the flux coefficients depend just on the water-surface height is only an approximation. In a compound channel, a more rigorous analysis might indicate that a rate of change of water-surface height also must be included. No studies that examine this problem are known. Therefore, the simple assumption is retained.
Critical flow is a function of the governing equation selected to represent the flow. The critical-flow value used must be consistent with the governing equation to avoid improper solutions. The physical meaning and interpretation of the computed critical flow must be established by observation and practice, as has been done for compact channel shapes in steady flow. In these cases, critical flow clearly defines a boundary in the physical system that has proven useful in describing various flow phenomena. The physical basis for critical flow computed for noncompact channels is less clear. Blalock and Sturm (1981) and Petryk and Grant (1978) have made some general observations, but no extensive body of experience is available to validate the physical interpretation of these estimates.
Because the momentum-conservation principle is used in FEQ to represent the 1-D flows, QM is the best estimate of critical flow. This estimate will be as consistent with the governing equations as possible. The effects of unsteadiness, however, cannot be included. Furthermore, representations of special features may be inconsistent (as described previously). The flow equations for some special features are based on energy-conservation principles. In most cases, however, the cross sections considered will be compact and simple, such as the barrel of a culvert, so that taking 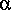= = 1 will be reasonable. For flexibility, the option of applying either equation 25 or 26 is available in the utility program, FEQUTL (Franz and Melching, 1997). For most flow conditions, equation 26 should be selected.
Another practical problem with the critical-flow estimates with flux-correction coefficients is that the critical flow may become undefined. In equations 25 and 26, the estimated rate of change of the flux-correction coefficient with respect to water-surface height may be such that the argument for the square root becomes negative. If the rate of change in the flux-correction coefficient is positive and large enough, the numerator in these equations can become zero or negative. The critical flow then becomes a complex number that is physically undefined. This can be a result of large inconsistencies between the estimated value of the flux-correction coefficient and the estimated rate of change with respect to water-surface height.