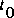 , and the equations are solved for the values at some time
, and the equations are solved for the values at some time 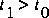 . Thus, the solutions for the time period of interest are developed stepwise in these methods.
. Thus, the solutions for the time period of interest are developed stepwise in these methods.
Full Equations (FEQ) Model for the Solution of the Full, Dynamic Equations
of Motion for One-Dimensional Unsteady Flow in Open Channels and Through
Control Structures
Computation of solutions for the equations of motion is necessarily limited to evaluating them at a finite number of points along the branch. The approaches to computing approximate solutions to these equations can be divided into two broad classes: those that fix the location of the points along the channel in advance and those that adjust the locations as needed in the solution. The latter class includes the broad range of the method of characteristics that solve the characteristic form of the equations by explicitly tracing the trajectories defined by equations 38 and 39 in whole or in part on the x-t plane. In the method of characteristics, the locations and times at which flows and elevations are computed are irregular and vary as the flow conditions vary. This method has some advantages in accuracy, but it becomes complex and impractical for use with prototype stream systems. Therefore, methods based on the characteristic form of the equations will not be considered further here because they are not used in FEQ.
The class of methods that uses a fixed set of locations (nodes) along the stream channel also is broad. This class divides into two subclasses: explicit methods and implicit methods. These methods offer practical advantages in that the locations of solution values in space and time are fixed. Thus, analysis and presentation of the results is simplified. In these methods, flow and elevation are assumed to be known at all locations at some initial time 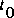 , and the equations are solved for the values at some time
, and the equations are solved for the values at some time 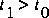 . Thus, the solutions for the time period of interest are developed stepwise in these methods.
. Thus, the solutions for the time period of interest are developed stepwise in these methods.
In explicit methods, the solution at time t1 at each node is computed in sequence with information at t0 within one or two distance intervals of the node. A pattern of points on the x-t plane used in some simple explicit methods is shown in
figure 12. The values are known at points
(65)
where
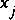 ,
, 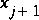 , and
, and 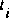 , and the method is applied to compute values at point G1 or point G2. The dashed characteristic trajectories show that the interval of dependence for point G1 is contained within the interval defined by
, and the method is applied to compute values at point G1 or point G2. The dashed characteristic trajectories show that the interval of dependence for point G1 is contained within the interval defined by  and
and  . Therefore, the flow conditions at point G1 can be computed. However, the interval of dependence for point G2 is larger than the interval defined by
. Therefore, the flow conditions at point G1 can be computed. However, the interval of dependence for point G2 is larger than the interval defined by 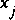 and
and 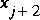 . Thus, it is impossible to compute the flow conditions at G2 given the information on the interval from
. Thus, it is impossible to compute the flow conditions at G2 given the information on the interval from 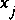 to
to 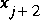 at time
at time 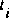 . The time step in the latter case is too large. In general, explicit methods have limitations on time steps. If these limitations are exceeded, the methods and (or) the computations become unstable, and the resulting flows and elevations will develop large non-physical oscillations and eventually the oscillations become so large that the computations fail because of negative depth, square root of a negative number, numerical overflow, and (or) other causes. The method is conditionally stable, however, if the time step meets certain constraints. The condition that generally applies is that the distance travelled by an infinitesimal wave in one time step must never exceed the distance between computational nodes. This is the Courant condition, given by
. The time step in the latter case is too large. In general, explicit methods have limitations on time steps. If these limitations are exceeded, the methods and (or) the computations become unstable, and the resulting flows and elevations will develop large non-physical oscillations and eventually the oscillations become so large that the computations fail because of negative depth, square root of a negative number, numerical overflow, and (or) other causes. The method is conditionally stable, however, if the time step meets certain constraints. The condition that generally applies is that the distance travelled by an infinitesimal wave in one time step must never exceed the distance between computational nodes. This is the Courant condition, given by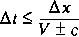 ,
,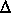 t is the computational time step.
t is the computational time step.
This constraint proves to be restrictive in that the time step is often limited to a few seconds, making extensive unsteady-flow computations with explicit methods impractical if long time periods (greater than a few hours) are simulated. Consequently, an explicit method is not used in FEQ.
Implicit methods solve for all of the unknowns at time 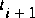 simultaneously. They are thus much more complex than explicit methods, which solve each nonboundary point independently of any other nonboundary point. The characteristic trajectories defined for an implicit method are shown in figure 13. The interval of dependence is larger than the interval of known conditions at time
simultaneously. They are thus much more complex than explicit methods, which solve each nonboundary point independently of any other nonboundary point. The characteristic trajectories defined for an implicit method are shown in figure 13. The interval of dependence is larger than the interval of known conditions at time 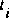 , but the boundary conditions supply the needed information. Thus, all the unknown points fall within the domain of uniqueness established by the characteristic trajectories beginning from the boundary points. Therefore, no restriction on the computational time step results from the nature of the shallow-water waves as in an explicit method. Implicit methods are not subject to the Courant condition for stability, so they are sometimes called unconditionally stable.
, but the boundary conditions supply the needed information. Thus, all the unknown points fall within the domain of uniqueness established by the characteristic trajectories beginning from the boundary points. Therefore, no restriction on the computational time step results from the nature of the shallow-water waves as in an explicit method. Implicit methods are not subject to the Courant condition for stability, so they are sometimes called unconditionally stable.
The stability of implicit methods allows use of large time steps in the solution. The time step may still be limited in terms of accuracy of results, but the time step can be adjusted to simulate varying flow conditions and not be restricted by the Courant condition. Implicit methods make it possible to simulate long time periods economically, with acceptable accuracy. Therefore, an implicit method called the Preissmann (1961) four-point scheme or method is applied in FEQ. This scheme has been used extensively with variations from the original form. Thus, the scheme as implemented in FEQ used only some of the concepts of the Preissmann method and might better be described as a weighted four-point scheme.
[Next Section]
[Previous Section]
[Table of Contents]