[Next Section]
[Previous Section]
[Table of Contents]
Full Equations (FEQ) Model for the Solution of the Full, Dynamic Equations of Motion for One-Dimensional Unsteady Flow in Open Channels and Through
Control Structures
U.S. GEOLOGICAL SURVEY WATER-RESOURCES INVESTIGATIONS REPORT 96-4240
9.4 Stability, Convergence, and Accuracy of the Solution Scheme
The results of any computation in steady or unsteady flow is an
approximation of flow in a stream system. The accuracy of the
approximation and the required accuracy for application in
decision making, design, or planning are complex questions.
Several concepts that relate to these questions are discussed in
this section.
The acceptability of the results must be considered in an
implicit comparison; that is, comparison of the results with
some other set of results either real or, if hypothetical, at
least obtainable if sufficient resources are available. The
performance of the mathematical model of the stream system
developed and computed with FEQ may be evaluated in the same
way as for measurements that have been made or could be made on
the prototype system. The key question relates to accuracy.
How close are the results to some standard? A related but
distinct concept is that of precision, the degree of refinement
in the result. A value can be precise without being accurate,
and an accurate result can be imprecise by certain standards.
A typical example relevant to open-channel flow analysis is the
reporting of elevations in surveys of stream cross sections.
Modern semiautomatic surveying systems commonly report
elevations to the nearest one-thousandth of a foot. At first
glance, the surveyed channel-bottom elevations appear accurate;
yet, in many cases, the elevations are only known within about
one-half foot because the leveling rod was placed on mud on a
channel bottom. On the flood plain, moving the point of
measurement a few feet will change the elevation by much more
than the precision of the measurement indicates.
The accuracy of the results is the primary interest, and
precision is usually not a limiting factor. However, accuracy
can be viewed as absolute or relative. Absolute accuracy is of
interest when the model is expected to reproduce the result as
measured in the prototype. For example, if measurements for a
major flood on a stream are available and are simulated in the
model, absolute accuracy is sought. Relative accuracy, on the
other hand, is applied for comparing differences between two
outcomes. An example would be evaluating the change in water
level resulting from the
construction of one or more reservoirs in a watershed.
Computing the change in water level resulting from different
structures on the stream can usually be done more accurately
than computing the water level. Typical applications of
unsteady flow often involve questions about the changes in
flows and water-surface elevations that result from planned
changes to watersheds or stream channels (for an example, see
Knapp and Ortel, 1992).
9.4.1 Truncation Errors
Every time a differential or integral equation is replaced with an
algebraic equation, a truncation error results. This is called a
truncation error because the infinite series has been truncated;
this also could be called the error of approximation that is
introduced because a finite number of terms is used to represent a
value requiring an infinite series solution. Finite steps are
taken in space and in time, and these errors relate to the size of
these steps and to the nature of the approximations used to
convert the continuous equations to discrete equations. The
truncation error is one of several attributes associated with a
numerical method.
A numerical method (also called a scheme) is consistent if the
continuous governing equations are obtained as both the time
and space increments approach zero. A numerical method is
convergent if the results obtained as both the time and space
increments are reduced approach a limiting value and that value
matches the true solution of the governing equations.
Consistency relates to the equations and convergence relates to
the solutions of these equations. A numerical method is
computationally stable if roundoff and truncation errors do not
accumulate such that the solution diverges.
A relation results among these concepts when the governing
equations are linear. In this special case, a stable,
consistent numerical method also is convergent. This is an
important result because it is often easier to demonstrate
stability and consistency than it is to demonstrate
convergence. In unsteady-flow analysis, however, the governing
equations are not linear, so this result does not rigorously
hold. Nevertheless, the numerical method used in FEQ
simulation is consistent and stable. Comparison of results as
the time and distance step are reduced can empirically verify
if the numerical method is convergent and that the time and
distance steps are small enough for the application.
For each branch in the model, one or more nodes within each
computational element defined in the branch description input
can be added with the ADDNOD option. If one
node is added, each computational element length is reduced by
half. Thus, the maximum time step should also be reduced by
one-half. Empirical tests for convergence involve computing a
series of solutions, denoted by
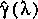 , where
, where 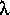 is a measure of the size of the time and
distance steps. If
is a measure of the size of the time and
distance steps. If 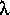 denotes the base level at which
the process of reducing the time and distance steps begins,
then the next level would be
denotes the base level at which
the process of reducing the time and distance steps begins,
then the next level would be 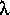 / 2 where the time
and space increments are one-half the base values. This
process can in principle continue to
/ 2 where the time
and space increments are one-half the base values. This
process can in principle continue to 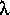 / 4,
l / 8, and so on. Values can be compared at node
locations common to all solutions to determine a trend toward a
common value. A trend provides empirical evidence that the
scheme is convergent. This process also can be applied to
adjust the time and space increments to reduce the truncation
errors if values are too high.
/ 4,
l / 8, and so on. Values can be compared at node
locations common to all solutions to determine a trend toward a
common value. A trend provides empirical evidence that the
scheme is convergent. This process also can be applied to
adjust the time and space increments to reduce the truncation
errors if values are too high.
In terms of storage requirements, model size grows in inverse
proportion to the size of the time and distance steps. Thus,
if the step size is one-fourth the base value, then the storage
requirement is increased about four times. The run time for a
simulation increases in inverse proportion to the square of the
step size. If the step size is again one-fourth of the base
value, then the run time will be about 16 times longer than
that for the base step. Therefore, limitations on
computational time and storage capacity are quickly
encountered. A way is needed to use only two such runs to
obtain some insight into the effect of varying the time and
space steps.
The Richardson extrapolation can be used with results from just
two model simulations for which time and distance steps
one-half the size of the first simulation are applied in the
second simulation. The approximations applied in FEQ
computations result in a truncation error being approximately
proportional to the square of the time and distance steps. A
reduction by half of both the time and distance steps should
reduce the errors by about one-fourth. This is true for the
time increment only if the value of the temporal integration
weight, WT, is close to 0.5. Let
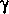 be the true solution at a given location;
then,
be the true solution at a given location;
then,
(137)
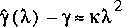
gives an estimate of the error, where  is
a constant
of proportionality. In the Richardson extrapolation, this
constant is assumed to be independent of the step size. Use of
this assumption results in
is
a constant
of proportionality. In the Richardson extrapolation, this
constant is assumed to be independent of the step size. Use of
this assumption results in
(138)
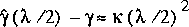
for the estimated error for the solution with the reduced step
size. This error is one-fourth the first error. Eliminating
the unknown constant of proportionality in equation 138 results
in
(139)
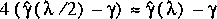 .
.
Solving this equation results in
(140)
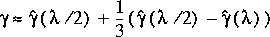 .
.
Therefore, a better approximation than either
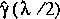 or
or
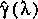 can be determined by correcting
can be determined by correcting
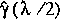 .
.
Application of equation 140 results in an error in the solution
with a corrected
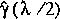 that is about one-third the difference between the two
solutions. The error in the solution for the larger time and
distance steps also can be estimated because, as shown in
equations 137 and 138, it is about four times the error in the
solution for the reduced time and distance steps. This cannot
be used as a correction as in equation 140, but it may
demonstrate that the error in
that is about one-third the difference between the two
solutions. The error in the solution for the larger time and
distance steps also can be estimated because, as shown in
equations 137 and 138, it is about four times the error in the
solution for the reduced time and distance steps. This cannot
be used as a correction as in equation 140, but it may
demonstrate that the error in
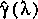 is small enough so that the model can be applied for the
intended purpose. This error is approximately 4/3 of the
absolute value of the difference between the two solutions. If
this error is acceptable, then the time and distance steps as
related to the truncation error also are acceptable.
is small enough so that the model can be applied for the
intended purpose. This error is approximately 4/3 of the
absolute value of the difference between the two solutions. If
this error is acceptable, then the time and distance steps as
related to the truncation error also are acceptable.
In the empirical convergence analysis applying the Richardson
extrapolation, the proportionality constant is assumed to be
virtually independent of the step size and neglected
higher-order terms are assumed to be small. This applies if
the initial step sizes are not too large. General guidelines
for selecting the initial time and distance steps are described
in the next few paragraphs.
Linear variation of values over each time and distance step is
assumed in FEQ computations. Appropriate step sizes should be
selected for this linear variation to be reasonable. The
matrix-solution method applied in FEQ computations is
unconditionally stable with respect to time step but not
unconditionally accurate. Small variations in the values of
flow at a boundary are often omitted when large time steps are
used. For example, if an inflow hydrograph has a 1-hour
duration of substantial flow, values for most of the hydrograph
will be missed if a 1-hour time step is applied. Therefore,
the maximum time step must be selected on the basis of
knowledge of expected flow variations.
The distance steps must be related to the water-surface height
of interest. A distance step appropriate for a small stream
with a maximum water-surface height of 3 ft will be much too
small for the main stem of a large river. On the lower
Mississippi River, distance steps of several miles may be
suitable because the variations in time and space are gradual
and the stream is more than 100 ft deep in many places. The
spacing of the nodes should be smaller where the water-surface
height is expected to vary rapidly; for example, near points of
critical or near-critical flow. Node spacing near critical
flow may be in the tens of feet or less. The spacing of nodes
also should be smaller where the channel changes shape or
roughness rapidly. The CHKGEO option in FEQ can be used to
identify possible regions of large variation in the channel
geometry. Initial steady-flow computations will fail where the
distance step is too long. If these requirements for
cross-section spacing are met and the frequency of culverts and
other controls in urban streams is considered, then the
distance steps for models of urban streams will likely be in
the appropriate range for accurate simulation.
Generally, the distance steps should be in the range of 100 to
300 times the water-surface heights of concern. Other
previously discussed constraints take priority over this range.
Choice of a time step such that 10 or more points are within
every flow event of concern also is appropriate. Once an
initial selection of time and distance steps has been made, the
empirical convergence testing can be applied to a typical part
of the stream to determine if the truncation errors are
acceptable. If model simulation is within the computational
capacity of the computer, full convergence testing of a typical
event also could prove useful.
9.4.2 Verification of the Accuracy and Convergence of the Full Equations Model
Typically, the accuracy and convergence of numerical models are
verified by use of simplified problems for which analytical
solutions are available. For unsteady flow, such analytical
solutions are not available. In the following paragraphs, the
accuracy and convergence of FEQ are demonstrated for unsteady,
free-surface flow in a sewer pipe by comparison with unsteady-flow
data collected in carefully controlled laboratory experiments done
at the Wallingford Hydraulics Research Station in England (Ackers
and Harrison, 1964). Two sets of simulations and experiments are
considered, one with raw data (experiment 115) and the other with
scaled data (data collected in the
0.25-ft diameter pipe and scaled up to a 1-ft diameter pipe by
Froude number equivalence principles). The scaled data were
derived by Ackers and Harrison (1964) to verify their method of
characteristics model of unsteady flow in open channels.
Hydraulic characteristics of the experiment and scaled
experiment used to verify FEQ are listed in table 4. For fully
turbulent flow, Manning's n is virtually constant for
a wide range of flow depths. The experiments done by
Ackers and Harrison (1964), however, include flow in the
transition region between laminar and fully turbulent flow.
Thus, Manning's n varies for the peak-flow and
base-flow conditions, as indicated in table 4. At present,
variations of Manning's n with depth are not
considered from a rigorous fluid-mechanics viewpoint in FEQ
computations because, for general applications, variations have
negligible effects on the accuracy of the overall routing of a
flood wave. The results of FEQ simulations discussed
subsequently use the Manning's n corresponding to the
base flow. For the scaled experiment, the difference in the
n values is negligible, whereas for experiment 115 the
wave is rapidly attenuated and flow is simulated acceptably for
all downstream locations by use of the higher n.

The results of the FEQ simulations are shown in a series of
graphs. The available data confine consideration to the
wave-peak depth and timing as the key test parameters. The
wave-peak depth plotted with distance is shown for experiment
115 in fig.22-
fig.23-
fig.24.
The convergence of FEQ calculations as a
function of the computation time step, 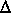 t, is
shown in figures 22- and
23. The magnitude of the wave-peak
depth is accurately simulated for
t, is
shown in figures 22- and
23. The magnitude of the wave-peak
depth is accurately simulated for 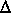 t
values of 6
seconds or less; thus, the model converged to the measured
depth with a
t
values of 6
seconds or less; thus, the model converged to the measured
depth with a 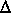 t as large as
one-sixth of the
duration of the input hydrograph. The convergence of the FEQ
calculations as a function of the computational distance step,
t as large as
one-sixth of the
duration of the input hydrograph. The convergence of the FEQ
calculations as a function of the computational distance step,
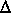 x, is shown in
figure 24. The magnitude of the
wave-peak depth is accurately simulated for
x, is shown in
figure 24. The magnitude of the
wave-peak depth is accurately simulated for 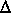 x
values of 50 ft or less. Thus, the model computations
converged to the measured depth with a
x
values of 50 ft or less. Thus, the model computations
converged to the measured depth with a 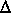 x as
large as one-sixth of the entire length of the test section.
The convergence of the FEQ calculations in terms of the timing
of the wave peak as a function of the computation distance
step,
x as
large as one-sixth of the entire length of the test section.
The convergence of the FEQ calculations in terms of the timing
of the wave peak as a function of the computation distance
step, 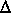 x, is shown in
figure 25. Even though the
x, is shown in
figure 25. Even though the
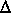 x of 50 ft yielded accurate results for the
wave-peak magnitude, the results are somewhat inaccurate in the
simulation of the timing of the wave peak.
x of 50 ft yielded accurate results for the
wave-peak magnitude, the results are somewhat inaccurate in the
simulation of the timing of the wave peak.
The instantaneous depth and time for five data-collection
locations in the scaled experiment are shown in
figures 26 and
27. The agreement between the measured and the simulated depth
at distances of 28.4 and 255.7 ft from the inlet is similar to
that achieved by Ackers and Harrison (1964) using their method
of characteristics model. Ackers and Harrison's model performs
somewhat better in depth simulation than FEQ for the more
downstream locations, because of a combination of the
depth-variable roughness and possible scaling problems.
The results presented here demonstrate that the numerical
scheme used in FEQ can converge to an accurate result with
relatively large space and time increments for unsteady flow in
a single branch. These computational results for single-pipe
laboratory experiments are encouraging with regard to
applications of FEQ to large,
multiple-branch, real-world stream networks.
9.4.3 Verification of the Full Equations model on the Fox River, Illinois
The accuracy of FEQ simulation also has been tested and verified
with field measurements for several stream systems. A
particularly thorough evaluation of the simulation accuracy
involved an application of FEQ to a 30.7mi reach of the Fox River
in northeastern Illinois (fig. 28), reported by Ishii and Turner
(1997). FEQ was tested and verified with stage, discharge, and
dye-transport data collected during a 12-day period of unsteady
flow induced by operations at the upstream boundary, a sluice-gate
control at Stratton Dam. The reach includes 19 bridges and 4
low-head overflow dams, including the dam at the downstream
boundary. The channel-bottom profile is shown in
figure 29. The
reach is effectively split into two subreaches on the basis of
slope. The upstream subreach, from Stratton Dam to Algonquin Dam,
has a bed slope of only 0.0034 percent and was subject to
considerable backwater effects and hysteresis in the
stage-discharge relations; the downstream subreach, from
Algonquin Dam to South Elgin Dam, has a bed slope of 0.039 percent
and was subject to little or no backwater effects. The channel is
virtually prismatic, with no trend in width from upstream to
downstream.
The study reach was represented in the FEQ model as a 45-branch
network. The number of branches was
determined by the number of bridges, dams, and tributary branch
inflows simulated. FEQUTL (Franz and
Melching, 1997) routines were used to compute the 2-D tables
for flow through the bridges and over the dams. The model of
the Fox River was developed by the Illinois Department of
Natural Resources, Office of Water Resources (IDNR-OWR) from a
HEC-2 model developed earlier by IDNR-OWR and the U.S. Amy
Corps of Engineers. The hydrology for the unmeasured tributary
inflows was done by proportioning a percentage of the measured
flow of the nearest of the two gaged tributaries among the
smaller tributaries by area. Only 26 percent of the
tributary-area flow was not measured at least once during the
verification field study.
The upper subreach of the model was calibrated by the Illinois
State Water Survey (Knapp and Ortel, 1992), and the lower
subreach was subsequently calibrated by IDNR-OWR. The upstream
boundary condition for the model calibration was discharge at
Wilmot Dam, 18.8 mi upstream from the study reach. Stage and
discharge data from two flood periods were used in the
calibration data set, and an additional six flood periods were
used to verify the calibration for the upstream reach. Seven
of the eight flood periods were used in the calibration of the
downstream reach.
The fully calibrated model was then passed to the USGS for
comparison to the measured stage and discharge data collected
during the unsteady-flow verification field study. No further
adjustment was made to the calibrated model during the
verification. All numerical results cited are from the
calibrated model with no adjustment. Adjustments in Manning's
n of -0.006 for the upstream reach and
+0.005 to the downstream reach were made and are clearly
indicated on the figures showing the calibrated results
(fig.
30), in order to demonstrate the effect of such an
adjustment. The verification periods differed from the
calibration periods in that flow was lower and no overbank
flooding resulted. The routed wave was a trough rather than a
peak. At locations where water-surface height was low, the
calibrated values for the roughness coefficient, Manning's
n, appeared to be too low compared to the effective field
values, resulting in simulated stages that were less than
measured stages by as much as 0.8 ft during the wave trough at
3 of the 15 locations where stage data were collected.
Simulated and field-measured stages were matched closely at the
other 12 sites, differences between the stages ranging from 0
to 0.3 ft. The routed discharge results were especially close
to field-measured values. The timing of the discharge
hydrograph and the stage hydrograph almost exactly matched the
observed hydrographs. The discharge and stage results at one
site in the upstream subreach and one site in the downstream
subreach are shown in figure 30.
The results at all sites are
presented in Ishii and Turner (1997).
At Huntley Road Bridge, 21.4 mi downstream from Stratton Dam
and 5 mi downstream from Algonquin Dam, a difference in the
hydrograph near the end of the wave trough is the result of
local rainfall that was not
simulated. Discharge is otherwise simulated accurately in both
timing and amount. The site is one of the three sites where
Manning's n appears to have been underestimated for
low flow. The stage-discharge relations at the same two sites
for the calibrated and adjusted simulations and the measured
values are shown in figure 31.
The hysteresis induced by the
variable-momentum slope in the upstream reach is clearly
evident. In contrast to this, the stage-discharge relation at
Huntley Road (in the downstream reach) shows little evidence of
hysteresis.
The study also included a semicontinuous dye injection with
manual and automatic collection of samples at 18 locations
during the unsteady-flow period. The velocity simulated in FEQ
was verified by inputting the
flow-field and dye-injection data to the Branched Lagrangian
Transport Model (BLTM) (Jobson and Schoelhammer, 1987) and
comparing the simulated and measured dye concentrations. The
match was acceptable given the limit of the temporal resolution
imposed by the relative infrequency of dye-sample collection at
most sites. The results for Fox River Valley Gardens and
Huntley Road Bridge are shown in
figure 32
together with the
measured and simulated discharges. Although the dye-injection
rate was almost constant, a spike in concentration resulted
from the higher concentration during the low-flow period. An
attenuated peak followed during the high-flow period. The
decline in concentration to near zero between the two peaks was
because of pump failure that resulted in a zero injection rate
for 15 hours between the two flow conditions.
Other results reported in Ishii and Turner (1997) include the
sensitivity of the model to computational and physical
parameters. Ishii and Wilder (1993) report on the results of
using different pairs of exterior boundary conditions. Turner
and others (1996) report on a study to verify the culvert and
overbank routines for a small stream reach. FEQ was determined
to be robust and accurate for these applications.
-
9.4.1 Truncation Errors
-
9.4.2 Verification of the Accuracy and Convergence of the Full Equations Model
-
9.4.3 Verification of the Full Equations model on the
Fox River, Illinois
[Next Section]
[Previous Section]
[Table of Contents]
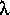 is a measure of the size of the time and
distance steps. If
is a measure of the size of the time and
distance steps. If 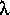 denotes the base level at which
the process of reducing the time and distance steps begins,
then the next level would be
denotes the base level at which
the process of reducing the time and distance steps begins,
then the next level would be 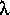 / 2 where the time
and space increments are one-half the base values. This
process can in principle continue to
/ 2 where the time
and space increments are one-half the base values. This
process can in principle continue to 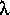 / 4,
l / 8, and so on. Values can be compared at node
locations common to all solutions to determine a trend toward a
common value. A trend provides empirical evidence that the
scheme is convergent. This process also can be applied to
adjust the time and space increments to reduce the truncation
errors if values are too high.
/ 4,
l / 8, and so on. Values can be compared at node
locations common to all solutions to determine a trend toward a
common value. A trend provides empirical evidence that the
scheme is convergent. This process also can be applied to
adjust the time and space increments to reduce the truncation
errors if values are too high.
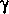 be the true solution at a given location;
then,
be the true solution at a given location;
then,
 is
a constant
of proportionality. In the Richardson extrapolation, this
constant is assumed to be independent of the step size. Use of
this assumption results in
is
a constant
of proportionality. In the Richardson extrapolation, this
constant is assumed to be independent of the step size. Use of
this assumption results in

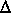 t, is
shown in
t, is
shown in