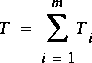
Full Equations Utilities (FEQUTL) Model for the Approximation of Hydraulic Characteristics of Open Channels and Control Structures During Unsteady Flow
The definitions of the characteristics of a cross section given in section 4 in the documentation report for the Full Equations model (Franz and Melching, 1997) are rigorous and exact if the boundary of the cross section is known exactly. This only applies for design computations for artificial channels. It does not apply for artificial channels as constructed because variations (acceptable and otherwise) from the design computations are always present. Concrete and steel closed conduits also have manufacturing tolerances as large as 2 percent from the nominal dimensions. Therefore, the characteristics of a cross section are always approximate. An approach for definition of the characteristics for a cross section is needed so that the approximations will be convenient, consistent, and sufficiently accurate. Franz (1982) presented a discussion of errors in approximation for static cross-sectional characteristics.
Channels of regular shape, such as trapezoidal, rectangular, and circular, can be represented by simple formulas. However, cross sections with regular shapes appear infrequently in most stream systems (excluding storm sewers). Furthermore, it is convenient to represent all cross sections in the same way. This is done in FEQ by application of a look-up table for the cross-sectional characteristics. A carefully defined table is not only convenient but also consistent and accurate. The development of a carefully defined table begins with a definition of the practical boundary of a cross section.
An example cross-section boundary with selected points on the boundary marked and connected with straight lines is shown in figure 1. In practice, the boundary of a cross section is specified by measuring the horizontal distance to points on the boundary at which elevation is measured. These points should, in theory, be selected so that the variation of the boundary between points is approximately linear and the assumption of linear variation is accurate. In all subsequent discussion, the boundary of the cross section is assumed to be represented by the polygonal shape established by connecting the surveyed points by straight lines. The degree of approximation depends on the skill of the survey crew in selecting measurement locations and in making measurements and can only be estimated by making another more detailed survey of the cross section with more points. In FEQUTL, the value of Manning's n (roughness coefficient) may vary from subsection to subsection. The subsections should be defined primarily on the variation of shape and Manning's n. The goal of subsection delineation is for each subsection to be hydraulically compact so that the hydraulic radius properly represents the shape in Manning's formula and the subsection conveyance may be correctly approximated. If the FEQUTL command FEQXEXT (section 5.9) is applied, Manning's n can vary in three ways within a subsection: (1) Each line segment composing the boundary of the subsection can have a different value of Manning's n. This represents variations of roughness within a subsection that is compact and probably should not be further subdivided. If the Manning's n for a line segment is zero, that line segment is excluded from the calculation of the wetted perimeter. A line-segment-weighted average of Manning's n is applied in FEQUTL to compute the conveyance in the subsection; (2) The user can define variation of Manning's n in the vertical direction with the hydraulic depth in the subsection as the argument for the variation; (3) The user can define variation of Manning's n in the vertical direction with the water-surface height as the argument.
Points of subdivision that account for changes in shape or boundary roughness are shown in figure 1. The boundaries between the subsections must be measured points on the cross-section boundary. The cross-section characteristic values are computed in FEQUTL in the following sequence of steps.
(2)
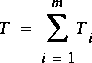
(3)

(4)
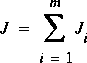
(5)
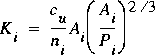
(6)
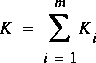
(7)
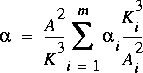
(8)
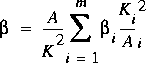
where
The integrals of velocity squared and velocity cubed over the flow (cross section) are approximated in equations 7 and 8 by a summation in
which it is assumed that the velocity in each subsection is given by ![]() ,
where Sf is the friction slope, and that the average velocity for the cross section is given by
,
where Sf is the friction slope, and that the average velocity for the cross section is given by
![]() . The friction slope is assumed to be the same for all
subsections and, therefore, is not in the final relations.
. The friction slope is assumed to be the same for all
subsections and, therefore, is not in the final relations.
The values of the momentum- and energy-flux correction coefficients in each subsection may be specified by the user or computed in FEQUTL.
The method utilized in computing the momentum- and energy-flux correction coefficients, 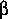 and,
and,
 in the cross section is specified with the parameter USGSBETA
(section 5.1). If USGSBETA= NO, then
in the cross section is specified with the parameter USGSBETA
(section 5.1). If USGSBETA= NO, then  =
=
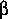 = 1.0 in each subsection of the cross section. If USGSBETA=YES,
then the values of
= 1.0 in each subsection of the cross section. If USGSBETA=YES,
then the values of  i and
i and 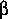 i are calculated as
i are calculated as  i = 14.8 ni + 0.884 and
i = 14.8 ni + 0.884 and
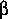 i = 1 + 0.3467(
i = 1 + 0.3467( i- 1),
where n i is the Manning's n in the subsection. The relation for
i- 1),
where n i is the Manning's n in the subsection. The relation for  was taken
from Hulsing and others (1966). The relation between
was taken
from Hulsing and others (1966). The relation between 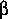 and
and  was computed by linear regression with unpublished data on
was computed by linear regression with unpublished data on 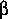 from the USGS that was computed but did not appear in Hulsing and others (1966)
NOTE 1. Only the values for compact cross sections were used here. The first relation has
considerable scatter relative to the data on
from the USGS that was computed but did not appear in Hulsing and others (1966)
NOTE 1. Only the values for compact cross sections were used here. The first relation has
considerable scatter relative to the data on  , but its application greatly improves the computation of the
value of
, but its application greatly improves the computation of the
value of  for the cross section. The second relation is well defined from the data with a correlation
coefficient of 0.996 and a standard error of estimate of 0.0066 for 87 pairs of
for the cross section. The second relation is well defined from the data with a correlation
coefficient of 0.996 and a standard error of estimate of 0.0066 for 87 pairs of  and
and
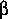 values computed from current-meter measurements in streams with approximately compact cross sections.
USGSBETA = YES should be used with caution because it was developed on the basis of a limited data set, and it has not been
verified computationally in detail. An alternative that may have better consistency is the NEWBETA option in FEQUTL, which is available
for most nonconduit channels. The NEWBETA option is discussed in section 3.1.2.
values computed from current-meter measurements in streams with approximately compact cross sections.
USGSBETA = YES should be used with caution because it was developed on the basis of a limited data set, and it has not been
verified computationally in detail. An alternative that may have better consistency is the NEWBETA option in FEQUTL, which is available
for most nonconduit channels. The NEWBETA option is discussed in section 3.1.2.
| Type 20: | y, T, A,
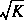 , , 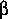
|
| Type 21: | y, T, A,
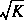 , , 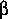 , J , J
|
| Type 22: | y, T, A,
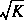 , , 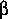 , J, , J,  , Q c , Q c
|
| Type 23: | y, T, A,
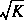 , , 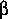 , MA, MQ , MA, MQ
|
| Type 24: | y, T, A,
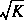 , , 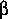 , J, MA, MQ , J, MA, MQ
|
| Type 25: | y, T, A,
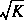 , , 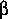 , J , , J ,  , Qc, MA, MQ , Qc, MA, MQ
|
Once the table is complete, it can be utilized to find values of the hydraulic characteristics at any water- surface height in the range of the table. Only a finite number of water-surface height values are tabulated, and intermediate values are determined in FEQ simulation by interpolation as described in section 11 in the documentation report for the Full Equations model (Franz and Melching, 1997).
Critical flow also is listed in tables of type 22 or 25. Several options are available for computing critical flow. If NEWBETA, NEWBETAM, or NEWBETAE are not specified, the critical flow is computed and tabulated ignoring the effect of velocity distribution. However, if NEWBETA, NEWBETAM, or NEWBETAE is specified, problems arise when differentiating equations 7 and 8 for the rate of change of the flux coefficients with respect to water-surface height in the cross section. A discontinuity in the derivative results at every breakpoint on the boundary of the cross section because the rate of change of the wetted perimeter with respect to water-surface height changes at each breakpoint. Furthermore, ignoring or smoothing this discontinuity may still result in frequent computation of an undefined critical flow because the denominator becomes negative in the relevant equations, namely
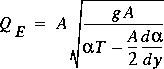
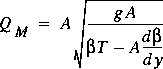
where
The use of subsection conveyance is too crude to define  and
and 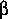 well enough for meaningful computation of
critical flow.
well enough for meaningful computation of
critical flow.
The options NEWBETA, NEWBETAM, and NEWBETAE are available in FEQUTL (sections 5.8 and 5.9) to include the effect of velocity distribution. Values are computed in the same manner in these options but different estimates of critical flow are tabulated. The inconsistencies between estimates of critical flow and the problems of determining critical flow indicate that a different method for estimating the flux coefficients should be developed. A first step in the development of a new method is an option for computing the flux coefficients for natural open channels available in FEQUTL. The new method is based on an approach suggested by Schönfeld (1951). In this approach, the depth-averaged velocities obtained by applying Manning's equation locally at each point across the cross section are integrated.
A typical line segment on the boundary of the cross section and the water surface above it are shown in figure 2. The boundary point on the left is denoted by the subscript L, and the boundary point on the right is denoted by the subscript R. These designations are used for any points of intersection between the boundary and the current water level. The slope of the boundary line, ms, is defined as
where z denotes elevation and s denotes
lateral position (offset) in the cross section at the
respective points L and R. The elevation of
a point on the boundary line at offset s where s
L  s
s  s R is
s R is
and the local height of the water surface, h, is given by
where z w is the elevation of the water surface.
In each vertical denoted by s, it is assumed that the
mean velocity,
v ( s ), is given by
where S A is the appropriate slope (energy slope, S e, or momentum slope, S f ) for the conservation principle considered, and the hydraulic radius is given by
 .
.
The inclusion of the slope of the boundary line in equation 15
approximately represents the reduced velocity at shallow depths
with sloping boundaries. For subsections with steep side
slopes the hydraulic radius is substantially smaller than the
depth when this approximation is applied. The friction or
energy slope term does not appear in the final result for  and
and 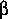 because it is the same throughout the
cross section and, thus, it is omitted from the following
equations for notational convenience.
because it is the same throughout the
cross section and, thus, it is omitted from the following
equations for notational convenience.
The following steps are applied in this method to estimate the flux coefficients and the critical-flow rate.
where the subscript i is omitted from the terms on the right-hand side to simplify the notation and
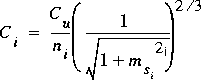 .
. If m s is not equal to zero, the integral in equation 16 is
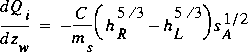 ;
; whereas if m s equals zero (that is h L equals h R ), the integral of equation 16 is
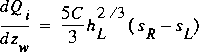 .
. ,
,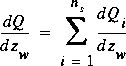 ,
,where n s is the number of line segments below the water surface. This flow estimate is applied only for the estimation of the flux coefficients, and it is never applied for estimation of the conveyance of the cross section.
where V ( s ) is the flow velocity at offset s in the cross section.
Substituting for the water-surface height and velocity from equations 13 and 14 yields
If m s is not equal to zero, equation 25 simplifies to
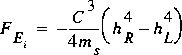 ,
, 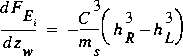 ;
;whereas if m s equals zero, equation 25 simplifies to
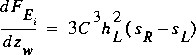 .
. 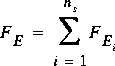 ,
, 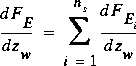 .
. Substituting for the depth and velocity from equations 13 and 14 yields
If m s is not equal to zero, equation 33 simplifies to
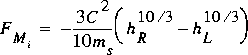 ,
, 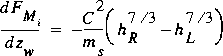 ;
; whereas if m s equals zero, equation 33 simplifies to
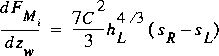 .
. 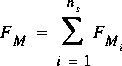 ,
, 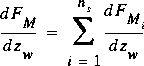 .
. 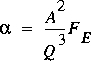
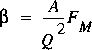
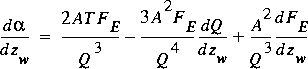
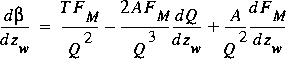 .
. 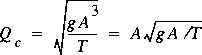 .
. If the NEWBETAE (sections 5.8 and 5.9) option is applied, Q E is tabulated. If the NEWBETAM (sections 5.8 and 5.9) option is applied, Q M is tabulated.
An undefined critical flow has not been encountered in application of this method to more than 300 natural cross sections. The method can still be improved because the two estimates of critical flow can be substantially different and the computed values of the flux coefficients are constant for some channel shapes. The local flux coefficient for each vertical is assumed to be one in the current version (1997) of the method.
The correction coefficients for channel curvilinearity, M A and M Q, are defined in equations 4 and 6 in Franz and Melching(1997) in terms of a limit involving the true volume of a slice of the channel. The equations defining M A and M Q are repeated here for convenient reference as
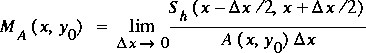
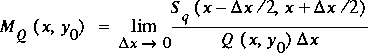 ,
,
where S h ( x 1, x
2 ) is the correct volume of water between cross
section at locations x 1 and x
2 for a given water-
surface height, y 0, and S q (
x 1, x 2 ) is the
correct momentum content of the flow between cross sections at
locations
x 1 and x 2
for a given water-surface height, y 0.
This slice of the channel is defined by placing cross sections
at a distance of 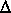 x /2 upstream and downstream
from a point x on the distance axis, where
x /2 upstream and downstream
from a point x on the distance axis, where 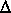 x
is the distance between cross sections. Every offset in
a section has a flow line passing through it, and by definition
each flow line is orthogonal to each cross section. Thus ,
x
is the distance between cross sections. Every offset in
a section has a flow line passing through it, and by definition
each flow line is orthogonal to each cross section. Thus ,
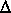 L ( s ) is defined as the distance
between the two cross sections at the upstream and downstream
faces of the slice at offset s. This incremental
distance is dependent on the offset and varies with the offset
but is independent of the local water-surface height, h
( s ). The true volume of this slice becomes
L ( s ) is defined as the distance
between the two cross sections at the upstream and downstream
faces of the slice at offset s. This incremental
distance is dependent on the offset and varies with the offset
but is independent of the local water-surface height, h
( s ). The true volume of this slice becomes
where an implicit water-surface elevation, z w,
with a water-surface height of y ( x ), is
assumed,
![]() is the average local water-surface height in the two sections,
and s B and s E are the starting
and ending points for the top width in the section at y
( x ). To include the possibility that the
cross-section boundary is above the water surface at some point
within the inundated limits, the local depth, h (
s ) = z w-z(s)
, becomes zero whenever z ( s )
is the average local water-surface height in the two sections,
and s B and s E are the starting
and ending points for the top width in the section at y
( x ). To include the possibility that the
cross-section boundary is above the water surface at some point
within the inundated limits, the local depth, h (
s ) = z w-z(s)
, becomes zero whenever z ( s ) 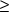 z w. Substitution of the volume in equation 47
into the definition for M A in equation 45 yields
z w. Substitution of the volume in equation 47
into the definition for M A in equation 45 yields
In the limit
![]() . The term
. The term 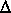 L ( s )/
L ( s )/ 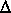 x is
the ratio of an incremental distance along a flow line to the
corresponding incremental distance along the axis. In the
limit
x is
the ratio of an incremental distance along a flow line to the
corresponding incremental distance along the axis. In the
limit 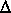 L ( s )/
L ( s )/ 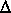 x becomes
the derivative of flow line distance to axis distance. This
derivative is the sinuosity of the channel and it may be
denoted by
x becomes
the derivative of flow line distance to axis distance. This
derivative is the sinuosity of the channel and it may be
denoted by 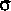 ( s ). As an
example, a sinuosity of 2.0 for a flow line means that at that
point the distance between adjacent cross sections will be
twice the distance between adjacent cross sections at the axis.
Substitution of these limits into equation 48 yields
( s ). As an
example, a sinuosity of 2.0 for a flow line means that at that
point the distance between adjacent cross sections will be
twice the distance between adjacent cross sections at the axis.
Substitution of these limits into equation 48 yields
where h ( s ) ds is a differential of area, dA. Also, the integral in equation 49 encompasses the entire wetted area of the cross section. Therefore, equation 49 can be expressed as
where integration is over area and the arguments for all the functions are dropped. Equation 50 is the same result as developed by DeLong (1989).
These same operations applied to equation 46 result in ,
, where q ( s ) ds is the differential for the total flow, dQ. Equation 52 also is the same result as developed by DeLong (1989).
In order to compute M Q, the local flow rate, q ( s ), must be defined. It is estimated using the local conveyance function, k ( s ), and the assumption that the decline in total energy-line elevation is constant along all flow lines that join two cross sections. The differential increment in the total energy-line elevation is dz e. Further, if the differential increment of distance on the axis is dx and the increment of distance on an arbitrary flow line is dx ( i ), then along an arbitrary flow line the local flow rate estimated in this manner is
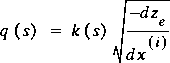 .
.
Application of M Q requires knowledge of q
for a given location in the cross section and for a given
decline of the elevation of the total-energy line as measured
along the axis; not along some arbitrary flow line. Thus, the
sinuosity is introduced by equating dx (
i ) to 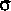 ( s ) dx
, and substituting
( s ) dx
, and substituting 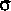 ( s ) dx
for dx ( i ) in
equation 53 yields
( s ) dx
for dx ( i ) in
equation 53 yields
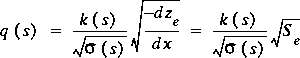 ,
, where S e is the energy slope as measured along the axis. Substitution of this definition of q ( s ) into equation 51 then defines the correction coefficient for channel curvilinearity effects on momentum content as
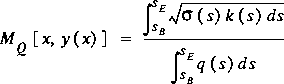 .
.The correction coefficients for channel curvilinearity and all the other hydraulic characteristics in the cross-section tables are computed in the CHANNEL command (section 5.2) in FEQUTL. M A and M Q are listed in tables of types 23, 24, and 25. In order to compute these characteristics for tabulation in a cross-section table, the sinuosity must be defined. Once sinuosity is defined for each cross section, equations 50 and 55 can be applied to compute the correction coefficients for any water-surface height desired. Two forms for the sinuosity are applied in FEQUTL: sinuosity that is piecewise constant (PWC ) over one or more subsections of a cross section, and sinuosity that is piecewise linear (PWL) between flow lines. PWC sinuosity is utilized to represent the sinuosity in cross sections derived from the Hydraulic Engineering Center Water Surface Profiles model, HEC-2, (U.S. Army Corps of Engineers, 1990a) data files and other sources that provide two or more distances between adjacent cross sections. These distances are defined as the mean flow distance, for example, on the left overbank, in the main channel, and on the right overbank. Thus, a flow line is not defined but rather an average distance is defined that represents the effect of all the flow-line distances between successive parts of adjacent cross sections. PWL sinuosity is utilized when specific flow lines are given and it is reasonable to assume that the sinuosity varies linearly between flow lines in a cross section. For PWC sinuosity, the mean flow lengths are treated as if measured from a line that is continuous through all cross sections. The computation of sinuosity is the same for both PWC and PWL variation with this interpretation; only the interpretation of the final values differs. For PWC variation, the sinuosity is the constant value that applies to the part of the cross section containing the mean flow line. For PWL variation, the sinuosity applies only at the intersection between the flow line and the cross section. Values of sinuosity for the cross section between flow lines are determined by linear interpolation.
Information is required in FEQUTL on two or more flow lines that pass through the cross sections for which function tables are being computed. The cumulative distance along each flow line to each cross section is input to or computed in FEQUTL from data supplied by the user. The cumulative distance along the i th flow line at the j th cross section is denoted as L ij. One of the flow lines will be the selected distance axis, which is specified by the user. The index for the axis is denoted by the subscript a in place of the index i; that is, L aj is the distance to the j th cross section on the distance axis. For a given flow line, the distance to successive cross sections is considered as a function of the distance to these same cross sections on the axis. This is the flow-line distance function. The sinuosity is the first derivative or slope of the flow-line distance function. Therefore, computation of the sinuosity is equivalent to computation of the first derivative of this function at each cross section. Thus, the sinuosity at the j th cross section on the i th flow line is
 .
.Computation of derivatives from crude numerical data, such as flow-line distances, can result in special problems. Four options are available in FEQUTL to define the sinuosity and give the user a large measure of control in the computation. These options are listed below.
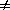 a. The sinuosity of the axis flow line is
always 1.0. An end condition is needed for the cubic
spline. The user can supply the sinuosity as an end
condition, or the end condition will be taken as a zero
value for the rate of change of sinuosity with distance
along the flow line. The second derivative of the flow-line
distance function is made zero at that point.
a. The sinuosity of the axis flow line is
always 1.0. An end condition is needed for the cubic
spline. The user can supply the sinuosity as an end
condition, or the end condition will be taken as a zero
value for the rate of change of sinuosity with distance
along the flow line. The second derivative of the flow-line
distance function is made zero at that point.
Once the sinuosities at each flow line and cross-section intersection are computed, the sinuosity function at each cross section, either PWC or PWL, must be defined. For computation, offsets for the boundaries of the subsections for the PWC variation and offsets at each flow line for PWL variation are required. These offsets are specified by the user. Extrapolation is applied if needed to extend the definition of sinuosity to whatever offset is required in the computations.
Any hydraulic characteristic that involves the distribution of the flow across the section will be affected by the sinuosity through q ( s ). This includes the conveyance and the flux-correction coefficients. The following adjustments apply if the sinuosity is PWC. Considering the effects of sinuosity, equations 6, 7, and 8 become
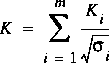
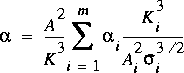
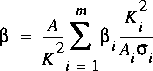 ,
,
where 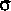 i is the sinuousity applicable to the
i th subsection in the cross section. The only change in
these equations from, equations 6, 7, and 8 is the inclusion of
the proper power of the sinuosity to reflect the change in
flow-rate distribution.
i is the sinuousity applicable to the
i th subsection in the cross section. The only change in
these equations from, equations 6, 7, and 8 is the inclusion of
the proper power of the sinuosity to reflect the change in
flow-rate distribution.
The equations for computing the correction factors for curvilinear elements are then
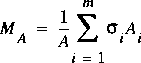 ,
, 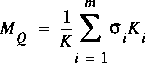 .
.
The integrals in the case of PWL sinuosity are more
complex, and closed-form expressions are long and complicated.
Therefore, numerical integration is applied in FEQUTL for the
integrals involved. The approach is similar to that used for
NEWBETA. In this case, however, the boundary points
input by the user are augmented with the points on the boundary
of the cross section wherever a flow line is placed. This
augmented list is then placed in ascending order of offsets
with all duplicate points deleted. This process results in a
series of distinct coordinate points on the boundary of the
section. Over the interval defined by consecutive points in
this series, both the local water-surface height,
h (
s ), and the sinuosity, 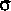 ( s ), are
piecewise linear functions of cross-section offset, s.
With the modification that the subscripts L and R
refer to the augmented boundary point series,, equations
11, 12, and 13 give the slope of the boundary, the boundary
elevation, and the local water-surface height, respectively,
for any point on any submerged line segment. As previously
discussed, the meaning of the subscripts L and R
is extended to include the intersection point for the
water surface with the boundary.
( s ), are
piecewise linear functions of cross-section offset, s.
With the modification that the subscripts L and R
refer to the augmented boundary point series,, equations
11, 12, and 13 give the slope of the boundary, the boundary
elevation, and the local water-surface height, respectively,
for any point on any submerged line segment. As previously
discussed, the meaning of the subscripts L and R
is extended to include the intersection point for the
water surface with the boundary.
The slope of the sinuosity for a submerged line segment, µ, on the cross-section boundary is defined as
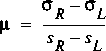 ,
, In terms of the constant, C, defined in equation 17, the local conveyance is
and the local flow rate q ( s ) is
The local velocity V ( s ) is given by q ( s )/ h ( s ).
The functions for the local sinuosity, conveyance, flow rate, and velocity are defined and continuous over any nonvertical, submerged line segment of the cross-section boundary that faces upward. Cross sections with converging sides are not permitted in these computations, and any vertical line segments are skipped because their lengths are not considered in the computed values. Three different functions and three different integrands are required in NEWBETA and related options. These functions define the flow rate, the flux of kinetic energy, and the flux of momentum above each submerged line segment; and, when combined with the derivatives of these functions with respect to the water-surface elevation, the information required in NEWBETA and related options is complete. The flows and fluxes as shown here do not contain the friction slope because it is a common factor to both the denominator and numerator of the final ratios of interest. Thus, the flows and fluxes are directly proportional to the same power of the friction slope with the power depending on the equation involved. The notation is the same as in equations 16, 24, and 32. The integrands and integrals involved are the following.
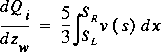
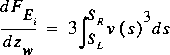 .
.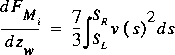 .
.
The values for each line segment are summed using equations 22, 23, 30, 31, 38, and 39 and the section values are computed with equations 40 through 43.
The numerical integration is done on the basis of a low-order Gauss rule. The same rule is applied for all the integrals so that each flux and its derivative are consistent. The correction factors for channel curvilinearity also are computed from equations 49 and 55 with the same Gauss rule.
If the NEWBETA options and PWL sinuosity are
requested, no segmentwide value of sinuosity is available to
adjust the subsection conveyance as required in equation 57. A
local-conveyance-weighted mean of
![]() within each subsection is computed and applied to adjust the
subsection conveyance for the effect of sinuosity to make this
adjustment consistent with the other values as defined under
NEWBETA.
within each subsection is computed and applied to adjust the
subsection conveyance for the effect of sinuosity to make this
adjustment consistent with the other values as defined under
NEWBETA.
A different approach can be utilized for the direct interpolation of the hydraulic characteristics of intermediate cross sections. The hydraulic characteristics may be interpolated in the cross-section table and without interpolation of the cross-section boundary. This permits the conveyance and other values that depend on the subsection boundaries to vary smoothly between measured cross sections. In the interpolation of intermediate cross-section tables in FEQUTL and FEQ the following rules are applied.
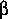 , the energy-flux correction
coefficient,
, the energy-flux correction
coefficient,  , the critical flow, and the
correction coefficients for channel curvilinearity vary
linearly with distance between cross sections when the
water-surface height is held constant.
, the critical flow, and the
correction coefficients for channel curvilinearity vary
linearly with distance between cross sections when the
water-surface height is held constant.
The tabulated water-surface-height values in the interpolated tables consist of the merged series of water-surface heights in the defining cross-section tables. In this way, no additional approximations are introduced in the intermediate cross sections. In FEQ simulation, the interpolation is restricted to be within the boundaries of a single branch, whereas in FEQUTL computation, the interpolation is restricted only to the confines given in the XSINTERP command (section 5.24) and is not limited to a single branch. Therefore, it is possible to define an interpolated cross section in FEQUTL computation to serve as the originating or terminating cross section for a branch in FEQ simulation.