[Next Section]
[Previous Section]
[Table of Contents]
Full Equations Utilities (FEQUTL) Model for the Approximation
of Hydraulic Characteristics of Open Channels and Control
Structures During Unsteady Flow
U.S. GEOLOGICAL SURVEY WATER-RESOURCES INVESTIGATIONS REPORT 97-4037
5.9 FEQXEXT Command
Purpose: Hydraulic characteristics of a cross section are computed
and a cross-section function table is output with the FEQXEXT
command. Frictionless line segments and roughness values that
vary with water level are included in FEQXEXT, and these features
represent an extension of the FEQX command.
Notes: A more flexible input for the cross-section boundary
points is available in FEQXEXT than in FEQX. In the FEQX
command, it is required that the line of information for each
boundary point (that is the line giving the offset, the
elevation, and the subsection number) be in a fixed order
(offset first, elevation second, and subsection number last)
and in fixed columns (1-10 for offset, 11-20 for the elevation,
and 21-25 for the subsection number).
A free format of boundary-point input is allowed in FEQXEXT,
but the fixed order is retained. A more complex description of
the variation of roughness on the channel boundary also is
permitted in FEQXEXT. Application of this more complex
description will add one or more values to each line of
information for a point on the cross-section boundary. To
distinguish the end of one value and the beginning of another
value, a delimiter is required in FEQXEXT. The delimiters
permitted are one or more spaces or a comma. All of the values
for a point must appear on a single line of the input.
Default values are available for much of the information in
FEQXEXT. For example, the default value for the subsection
number for all but the first point on the boundary is the
number for the preceding point on the boundary. The subsection
number needs to be given only for the first point in each
subsection.
The roughness for each line segment on the boundary may be
specified in FEQXEXT, not just each subsection as in FEQX.
This value appears after the subsection number in the input.
If the default value for the subsection
number is to be used by omitting the number for a boundary
point, then an asterisk must be used to request the default
value, or two consecutive commas must be used to indicate the
place that the subsection number would have occupied had it
been given. If this is not done, the line-segment roughness
value will be taken as being a
subsection number because it is the third value seen on the
line of input. The third value is always the subsection
number. The asterisk or the dual commas indicate that the
third value and the line-segment roughness value are given the
proper input order.
In general, any value that has a default that is skipped over
in a line must have its place shown by either an asterisk or by
a pair of commas. If this is not done, the results of the
command will be in error and an error message may be issued.
LINE 1
Variable: TAB, CIN
Format: 7X, I5, A50
Example: TABLE #= 00025 MONOTONE SAVE22
Explanation:
|
TAB is the table number that identifies the cross-section
function table computed from the cross-section boundary
description specified in the subsequent lines.
CIN is an alphanumeric field in which the user may specify
several options after the table number. The options are as
follows.
EXTEND: A vertical, frictionless extension is added to the first
or last point of the cross section, as needed, to match the
point of maximum elevation in the cross section.
MONOTONE: The offsets for the cross section are examined to
ensure that they are increasing. This is useful in preliminary
checking of cross sections for natural streams.
NEWBETA: The momentum-flux correction coefficient, 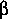 ,
and the kinetic-energy-flux correction coefficient, ,
and the kinetic-energy-flux correction coefficient, 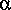 ,
are computed by application of a method suggested by Schönfeld (1951) and
discussed in section 3.1.2. The geometric mean of the critical
flows estimated with the momentum and energy principles are
tabulated in this option. ,
are computed by application of a method suggested by Schönfeld (1951) and
discussed in section 3.1.2. The geometric mean of the critical
flows estimated with the momentum and energy principles are
tabulated in this option.
NEWBETAE: Same as NEWBETA except that the critical flow
tabulated is based on the energy principle.
NEWBETAM: Same as NEWBETA except that the critical flow
tabulated is based on the momentum principle.
NEWBETA, NEWBETAM, and NEWBETAE can only be used for cross
sections that do not have converging boundaries. Thus, these
options imply checking for monotonicity.
OLDBETA: The coefficients 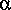 and and 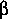 for the
cross section are computed from equations 7 and 8 in section
3.1.1. The velocity-distribution coefficients, for the
cross section are computed from equations 7 and 8 in section
3.1.1. The velocity-distribution coefficients, 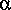 i
and i
and 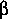 i in each subsection of the cross
section in these equations are taken to be 1.0 if USGSBETA
= NO in the Standard Header Block (section 5.1). If
USGSBETA=YES, then these coefficients are estimated as
described following equation 8 in section 3.1.1. In either
case, the critical flow in the cross section is estimated as if
the velocity distribution coefficients are both 1. Thus,
critical flow is computed ignoring the effect of velocity
distribution. i in each subsection of the cross
section in these equations are taken to be 1.0 if USGSBETA
= NO in the Standard Header Block (section 5.1). If
USGSBETA=YES, then these coefficients are estimated as
described following equation 8 in section 3.1.1. In either
case, the critical flow in the cross section is estimated as if
the velocity distribution coefficients are both 1. Thus,
critical flow is computed ignoring the effect of velocity
distribution.
SAVEnn: A copy of the resulting table is saved internally in the
FEQUTL computations in type nn format, where nn gives the
two-digit table type with the valid range from 20 through 25.
SAVE: Same as SAVE21.
NOSAVE: A copy of the table is not saved internally in the
FEQUTL computations. This is the default action if none of the
save options are given.
OUTnn: A copy of the table is output to the standard
function-table file in the Type nn format. If no output option
is given, a cross-section function table of type 21 is output
to the standard-function table file.
NOOUT: Output of the table to the standard function-table file
is suppressed.
|
LINE 2
Variables: STAT, LEFT, RIGHT
Format: 8X, F10.0, 6X, F10.0, 7X, F10.0
Example: STATION = 8.256 LEFT = 100.0 RIGHT
= 967.
Explanation: |
STAT is the station of the cross section.
LEFT is the offset on the left side of the cross section where
a vertical frictionless wall is added in computation of the
cross section.
RIGHT is the offset on the right side of the cross section
where a vertical frictionless wall is added in computation of
the cross section.
|
Thus, encroachments on the cross section can be indicated
without changing the cross section. If LEFT 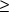 RIGHT, then the encroachments are not calculated. LEFT is set
equal to RIGHT by default if the input is omitted.
RIGHT, then the encroachments are not calculated. LEFT is set
equal to RIGHT by default if the input is omitted.
LINE 3
Variables: VARN, SCALE, SHIFT
Format: 5X, A4, 7X, F10.0, 7X, F10.0
Example: VARN = NCON SCALE = 1.0 SHIFT =
0.2
Explanation: |
VARN specifies the variation of Manning's n .
Three options are available for VARN:
NCON-constant n; HYDY- n varies with
hydraulic depth in each subsection; MAXY- n varies
with maximum water-surface height in each subsection. HYDY is
the default option for VARN.
SCALE is multiplied with the offsets and can be used to adjust
for scaled measurements from a map. The default value is 1.
SHIFT is added to elevation of each point on the boundary of
the cross section. The default value is 0.
|
LINE 4
Variables: NSUB, N(1),...,N(NSUB)
Format: 4X, I5, 6F10.0,/,(9X, 6F10.0)
Example: NSUB 3 0.03 0.02 0.04
Explanation: |
NSUB is the number of subsections. The valid range for NSUB is
from 1 to 96.
N( i ) is Manning's n for each subsection for
the cross section.
|
The divisions between subsections are defined by frictionless,
vertical lines.
LINE 5
Variable: HEAD
Format: A80
Example: OFFSET ELEVATION SUB N0 Y1 N1 Y2 N2 Y3 N3 Y4 N4
Explanation:
|
HEAD is a user-defined heading to describe the information on
subsequent lines. No fixed columns are given for subsequent
input, only a fixed order. Therefore, the headings can be
spaced for user convenience.
|
LINE 6 (Repeated for each point on the boundary.)
Variables: X( i ), Z( i ), SB( i ),
N0( i ), (YATN, NATY)(*, i )
Example 1: -20.0 675.0 1 0.032
Example 2: -20.0 600.0 * 0.050 20.0 0.035
Explanation:
|
X( i ) is the offset of the coordinate point i
on the boundary of the cross section.
Z( i ) is the elevation of the coordinate point i
on the boundary of the cross section.
SB( i ) is the subsection number for the coordinate
point i on the boundary of the cross section.
N0( i ), YATN, NATY are parameters used to describe
the variability of Manning's n with respect to
water-surface height and position in the cross section. The
definition of these variables changes depending on the
specification of VARN on Line 3 as described in the following
discussion.
-
If VARN = HYDY or VARN = MAXY,
- N0 is the value of Manning's n at a zero value of
water-surface height in a subsection. YATN is the value of
hydraulic depth (HYDY) or maximum water-surface height (MAXY)
at which a value of the variable Manning's n is
specified.
In this case, N0 as well as YATN and NATY can only be given at
the first point of each subsection. The variation of Manning's
n is specified by five points: one at zero
water-surface height and four others at user-defined levels in
each cross section. Linear variation of the n value
with water-surface height (hydraulic or maximum) is assumed in
each subsection. The values of water-surface height given for
the variation of Manning's n in each subsection must
be increasing. If VARN = HYDY or VARN =
MAXY, but N0 is not given, then the value of N0 from the
subsection n value is utilized in FEQXEXT. Moreover,
if N0, YATN, and NATY are omitted, the roughness is assumed to
be constant for all subsections at the value given for the
subsection in the FEQXEXT computations.
- If VARN = NCON or if no data are given for vertical
variation of roughness,
-
a wetted-perimeter weighted composite roughness value in each
subsection is computed in FEQXEXT. If N0 = 0 for a
line segment, that line segment is treated as frictionless in
the
computation of the composite roughness value.
|
It is possible to have four different modes of variation of
roughness in a cross section. The first is no variation. The
second is variation with the hydraulic depth in the subsection.
The third is variation with the maximum water-surface height in the cross section.
The fourth and last
variation is in the composite value of n as the water
level in the subsection changes. Not all combinations can
result in a cross section simultaneously. However, three of
the four combinations can be used simultaneously in a single
cross section, if necessary.
The last point on the cross-section boundary is indicated by a
subsection number of -1. This convention means that
the subsection number for a point applies to the line segment
connecting the point to the subsequent point. Thus, a
subsection assignment is not required for the last point
because no line segment is present between it and a subsequent
point. Therefore, the subsection for the last point is used in
FEQUTL as a flag to signal the end of the cross-section
specification.
The minimum data for the first point of a cross-section
boundary are the offset, elevation, and subsection number. The
minimum information for all subsequent points is offset and
elevation. If more than one subsection is required to describe
the cross-section boundary, then a subsection number must be
added at the first point in each of the subsections after the
first.
A conduit-closed section can be specified by defining the
offsets and elevations of points around the perimeter of the
section. The description should begin at the high point of the
section and should not close completely so that a free surface
remains. The closed-conduit section should be traversed in a
counterclockwise direction when defining points on the
boundary.
Some users have used the columns after the subsection number
for a boundary point in the command FEQX for comments about the
source of the data for that point. These could include the
state plane coordinates of that point, the nature of the point,
and related information. The line is not read beyond the
subsection number columns in FEQX. However, the entire line is
read in FEQXEXT. In order to support these comments, the
remainder of a line after the single quote character (') is not
read in FEQXEXT. Thus, it becomes possible, where needed, to
utilize FEQXEXT and still maintain the unsupported comments on
the line.
[Next Section]
[Previous Section]
[Table of Contents]
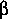 ,
and the kinetic-energy-flux correction coefficient,
,
and the kinetic-energy-flux correction coefficient, 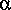 ,
are computed by application of a method suggested by Schönfeld (1951) and
discussed in section 3.1.2. The geometric mean of the critical
flows estimated with the momentum and energy principles are
tabulated in this option.
,
are computed by application of a method suggested by Schönfeld (1951) and
discussed in section 3.1.2. The geometric mean of the critical
flows estimated with the momentum and energy principles are
tabulated in this option.
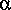 and
and 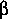 for the
cross section are computed from equations 7 and 8 in section
3.1.1. The velocity-distribution coefficients,
for the
cross section are computed from equations 7 and 8 in section
3.1.1. The velocity-distribution coefficients, 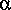 i
and
i
and 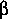 i in each subsection of the cross
section in these equations are taken to be 1.0 if USGSBETA
= NO in the Standard Header Block (section 5.1). If
USGSBETA=YES, then these coefficients are estimated as
described following equation 8 in section 3.1.1. In either
case, the critical flow in the cross section is estimated as if
the velocity distribution coefficients are both 1. Thus,
critical flow is computed ignoring the effect of velocity
distribution.
i in each subsection of the cross
section in these equations are taken to be 1.0 if USGSBETA
= NO in the Standard Header Block (section 5.1). If
USGSBETA=YES, then these coefficients are estimated as
described following equation 8 in section 3.1.1. In either
case, the critical flow in the cross section is estimated as if
the velocity distribution coefficients are both 1. Thus,
critical flow is computed ignoring the effect of velocity
distribution.
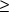 RIGHT, then the encroachments are not calculated. LEFT is set
equal to RIGHT by default if the input is omitted.
RIGHT, then the encroachments are not calculated. LEFT is set
equal to RIGHT by default if the input is omitted.