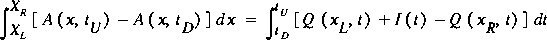 .
.
Full Equations (FEQ) Model for the Solution of the Full, Dynamic Equations
of Motion for One-Dimensional Unsteady Flow in Open Channels and Through
Control Structures
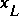 is assumed to be orthogonal to the flow direction at that point in the channel, as outlined previously. The downstream face of the control volume at station
is assumed to be orthogonal to the flow direction at that point in the channel, as outlined previously. The downstream face of the control volume at station 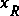 also is assumed to be orthogonal to the flow direction. The sides and bottom of the control volume are formed by the sides and bottom of the channel. The top of the control volume is formed by the water surface. The length of the control volume,
also is assumed to be orthogonal to the flow direction. The sides and bottom of the control volume are formed by the sides and bottom of the channel. The top of the control volume is formed by the water surface. The length of the control volume, 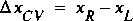 , does not have to be small and is measured along the distance axis defined previously.
, does not have to be small and is measured along the distance axis defined previously.The integral form of the equations can be explained simply in a 1-D approximation; therefore, the equations are presented here without derivation, followed by discussion of what each major term or set of terms represents in the conservation principle. To keep the details as simple as possible, the weight coefficients used to correct certain integrands in the integral form for the effects of curvilinear flow are omitted at first. These weights are added later when the full form of the equations is developed for curvilinear channel alignments.
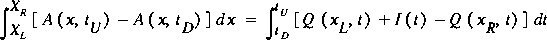 .
.
The time interval of integration is defined by two points in time,  and
and 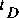 , such that
, such that 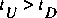 . (The meaning of the subscripts on these time points is explained in more detail in subsequent sections.) The term I(t) denotes the inflow of water that enters the control volume over or through the sides of the channel. Density is constant and is not shown in equation 27 because each term would have a constant multiplier that cancels from the relation. Thus, the conservation of mass is equivalent to conservation of water volume in FEQ simulation. Equation 27 is a precise mathematical statement of a simple concept. The left-hand side of equation 27 is the change in volume of water contained in the control volume during the time interval
. (The meaning of the subscripts on these time points is explained in more detail in subsequent sections.) The term I(t) denotes the inflow of water that enters the control volume over or through the sides of the channel. Density is constant and is not shown in equation 27 because each term would have a constant multiplier that cancels from the relation. Thus, the conservation of mass is equivalent to conservation of water volume in FEQ simulation. Equation 27 is a precise mathematical statement of a simple concept. The left-hand side of equation 27 is the change in volume of water contained in the control volume during the time interval 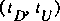 . The integral of flow area with respect to distance at a fixed time defines the volume of water in the control volume at that time. The right-hand side of equation 27 is the net volume of inflow to the control volume (inflow minus outflow) during the time interval. Water enters from upstream,
. The integral of flow area with respect to distance at a fixed time defines the volume of water in the control volume at that time. The right-hand side of equation 27 is the net volume of inflow to the control volume (inflow minus outflow) during the time interval. Water enters from upstream, 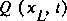 , leaves downstream,
, leaves downstream, 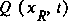 , and enters over or through the sides of the channel, I(t). Thus, equation 27 indicates that the change in volume of the water in the control volume during any time interval is equal to the difference between the volume of inflow and the volume of outflow during that time interval. The term I(t) represents what is commonly called the lateral inflow, which comes from several sources: runoff from the land surface, discharges from sewers, outflows of water from pumping, and others. If the lateral flow is out of the channel, then I(t) is negative.
, and enters over or through the sides of the channel, I(t). Thus, equation 27 indicates that the change in volume of the water in the control volume during any time interval is equal to the difference between the volume of inflow and the volume of outflow during that time interval. The term I(t) represents what is commonly called the lateral inflow, which comes from several sources: runoff from the land surface, discharges from sewers, outflows of water from pumping, and others. If the lateral flow is out of the channel, then I(t) is negative.
To satisfy the conservation principle, the change in momentum of the water in the control volume over any time period must be equal to the net downstream impulse during the time period plus the net flux of momentum during the time period (that is, influx minus efflux). Impulse is a time integral of a force. In most basic fluid mechanics texts (for example, Streeter and Wylie 1985, p. 117), the conservation of momentum for a control volume in one dimension, x, is expressed as

where
|
Fx are the forces acting on the control volume, CV;
vx is the velocity in the x-direction; d 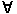 is the volume differential; is the volume differential;
V is the velocity vector; and dA is the differential area taken as a vector normal to the control surface, CS, of the control volume. |
For open-channel flow, the forces included are pressure forces on the upstream and downstream faces, downstream component of the pressure force on the sides of the channel, gravity force, channel friction, and wind-shear stress on the water surface. By moving the momentum stored in the control volume to the left-hand side and the sum of forces to the right-hand side and expanding the sum of forces, the conservation of momentum for the control volume becomes
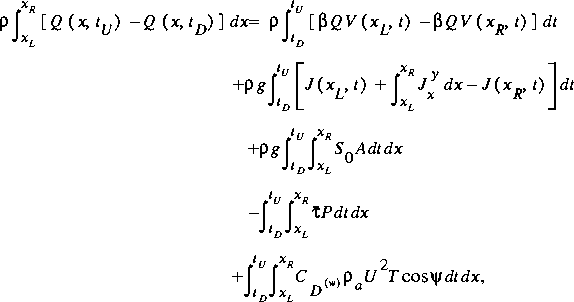
where
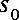 is the bottom slope of the channel, is the bottom slope of the channel,
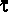 is the average shear stress on the water from the channel boundary, is the average shear stress on the water from the channel boundary,
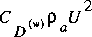 is the wind-induced shear stress on the water surface in the direction of the wind-velocity vector, is the wind-induced shear stress on the water surface in the direction of the wind-velocity vector,
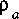 is the density of air, is the density of air,
U is the wind velocity, 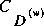 is the dimensionless drag coefficient for wind shear stress, and is the dimensionless drag coefficient for wind shear stress, and
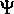 is the angle between the downstream flow direction in the channel and the velocity of the wind. is the angle between the downstream flow direction in the channel and the velocity of the wind.
|
The integral on the left-hand side of equation 29 is a rewritten form of the change in momentum stored in the control volume. The downstream component of the pressure force on the sides of the channel also is given by integration with respect to distance of the force per unit length discussed previously. The gravity force is represented by the integration of the product of fluid density and area (the mass per unit length of channel) and the bottom slope of the channel. The friction force per unit length is given by the product of the shear stress and the wetted perimeter. The friction force per unit length is then integrated over the length of the control volume to yield the friction force at any time. The wind-shear stress per unit length of the channel is given by the product of the wind-shear stress in the direction of the channel and the top width of the channel. Integration with respect to distance yields the total wind-shear force at any time. The influx and efflux of momentum are represented by the first integral to the right of the equal sign in equation 29. The time integration of the distance integrals for the forces on the control volume yield the impulses from these sources. The arguments affecting the elements integrated with respect to both time and distance in equation 29 are not shown to simplify the notation. The arguments of time and of distance are both implicit in these instances.
Although complicated, the integral equation (eq. 29) is a precise mathematical statement of the conservation of momentum principle; specifically, that the change in momentum of the water in the control volume is given by the net influx of momentum and the net downstream impulse from all forces acting on the water in the control volume. Given the selection of forces and other assumptions, equation 29 is an exact statement that applies for any length of control volume.
The friction-force term simplifies if it is assumed that the relation between slope and boundary friction from steady-uniform flow,
(30)
 ,
,
can be generalized to unsteady flow by replacing the bottom slope, 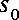 , with the friction slope,
, with the friction slope, 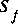 . Applying this definition of the friction slope and dividing equation 29 by
. Applying this definition of the friction slope and dividing equation 29 by 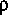 results in
results in
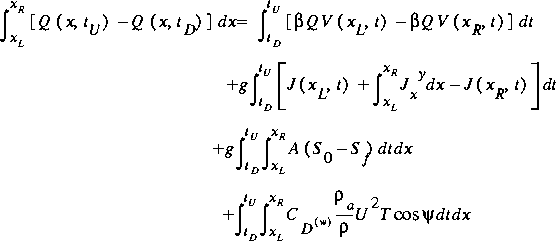
as the integral form for the conservation of momentum equation for open-channel flow. This and related equations are called motion equations. In equation 31, the momentum contribution from the lateral inflow is ignored. Reliable information is rarely available regarding the velocities and depths of lateral inflows, and lateral inflows are often nearly orthogonal to the flow in the channel. Thus, omitting the effects of lateral inflow in equation 31 should not result in substantial error.
The friction slope must be estimated from the cross-sectional characteristics and the flow. In terms of the total channel conveyance, K, the friction slope is computed from
(32)
 .
.Use of the product Q|Q| instead of Q2 as normally seen in steady-flow analysis gives the result that the friction is a retarding force on the water in the control volume for either direction of flow. Therefore, the possibility of reversing flows is simulated in FEQ.