[Next Section]
[Previous Section]
[Table of Contents]
Full Equations Utilities (FEQUTL) Model for the Approximation
of Hydraulic Characteristics of Open Channels and Control
Structures During Unsteady Flow
U.S. GEOLOGICAL SURVEY WATER-RESOURCES INVESTIGATIONS REPORT 97-4037
4.8 Underflow Gates
The flows through a sluice gate or a tainter gate are approximated
in FEQUTL by computing a series of 2-D tables: one table for
each of a series of gate openings. When the gate opening is
fixed, the flow is defined for given upstream and downstream
water-surface elevations. The 2-D tables are of type 13. This
requires that a drop is present from the upstream water surface to
the downstream water surface. This should be applicable in most
cases. These tables are computed in the UFGATE command (section
5.20). A 1-D table of type 15 is used to store the gate openings
and the corresponding table numbers for the 2-D tables. Thus, a
3-D table look-up is done in FEQ simulation to define the
hydraulics of a sluice or tainter gate.
A sketch of the cross sections used to define the gate and its
approach and departure channels is shown in figure 15. A
sketch of the various flow conditions that may result for an
underflow gate at a fixed gate opening is shown in figure 16.
The flow through the gate is zero when the piezometric head at
section 1 is the same as the piezometric head at section 4.
The flow is grouped into four classes or conditions as
identified in Fisk (1988):
free and submerged orifice and weir flows. Free-orifice flow
(FO) results when flow in contact with the gate lip is
unaffected by downstream water level. Free-weir flow (FW)
results whenever the gate lip is free of the water
surface and the flow is unaffected by downstream water levels.
The transition between the two flow conditions results when the
upstream piezometric head at section 1 exceeds the gate-lip
elevation enough to raise the water at section 2 to the gate
lip. The boundary between these two flow conditions is shown
as a vertical dashed line in figure 16. If the piezometric
head at section 1 is held at a fixed value and the downstream
water-surface elevation at section 4 is increased enough, the
flow through the gate will be submerged. If the gate lip is in
contact with the water, the flow condition is denoted as
submerged orifice (SO). If the gate lip is free and
subcritical flow is present at the weir, the flow condition is
denoted as submerged weir (SW). The regions for these flow
conditions are shown in figure 16 with the boundaries between
regions represented by dashed lines. The assumptions made in
the analysis applied in FEQUTL result in the transitions as
shown in figure 16. The boundaries between the four regions
meet at a single point.
The key assumptions, not including the 1-D flow assumption,
made in the analysis of underflow gates are as follows.
-
The departure channel, from section 3 to section 4 in figure
15, is assumed to be horizontal and prismatic so that a
simple momentum balance can be used to estimate the
submergence of the flow through the gate openings. This
assumption has been used with reasonable success by Henry
(1950) and Rao and Rajaratnam (1963).
-
At least a small contraction in the flow area between the
approach section (section 1) and the gate openings is always
present. Generally, the appurtenances needed for the
mounting and movement of the gates make this necessary.
This means that the flow is contracting as it moves from
section 1 to section 2 even if the gates are raised to the
maximum position and are not in contact with the water.
-
The floor of the departure reach is at or below the floor of
the approach reach. If a step is present, it is as shown in
figure 15.
-
Submergence of the flow through the gate begins as soon as
the estimated depth at the point of minimum contraction of
the emerging jet is exceeded by the water-surface elevation
at section 3. Sections 2 and 3 are taken at essentially the
same point with section 2 describing the emerging jet and
section 3 describing the conditions at the upstream end of
the departure reach.
-
The size of the emerging jet is approximately the same in
both free-flow and submerged-flow conditions. For cases of
orifice flow, the jet size is given by C coh
g, where C co is a contraction
coefficient and h g is the gate opening. This
is not always true, but utilization of this assumption for
underflow gates by Henry (1950), Toch (1955), and
Elevatorski (1958) produced good results.
-
FW flow is computed assuming that critical flow results in
the gate opening. This avoids the need for estimating a
weir coefficient for this condition.
-
The submergence of the flow for both FO and FW conditions is
computed based on a simple momentum
balance. Smooth transitions between different flow
conditions may be obtained with a simple momentum
balance.
-
The coefficient of contraction for sluice gates is a
function of the ratio of the gate opening to the approach
piezometric head, called the gate-opening ratio. The
coefficient of contraction for tainter (radial) gates is
taken to be a function of the angle that the upstream face
of the gate lip makes with the horizontal plane (Toch,
1955).
-
Transitions between the flow classes are smoothed by varying
the contraction coefficient from the value of 1.0 at the
weir-flow (FW or SW) limit when the water just touches the
gate lip to the contraction-coefficient value for orifice
flow (FO or SO). The smoothing takes place over the
interval h 1fwul to h
1fwul + R hg h
g = h1foll,
where h 1fwul gives the upper
limit for piezometric head at section 1 for FW flow; h
1foll gives the lower limit of FO
flow with a standard coefficient of contraction; and R
hg is the fraction of the gate opening width over
which the transition in contraction coefficient is applied.
The variation is taken to be linear as a function of the
head at section 1. In addition, C co is
1.0 for the small region of SO flow that is above the SW
flow region between hp1=hg and hp1 = h1fwul
in figure
16. The user controls the abruptness of the transition by
selection of the value of Rhg.
4.8.1 Free-Orifice Flow
Utilizing a simple energy relation between sections 1 and 2 and
allowing for some loss of energy with a
discharge coefficient, C dfo, yields the governing
equation for FO flow
(106)
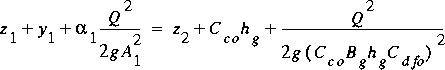 ,
,
where B g is the width of the gate opening; and
z j is the elevation of the channel bottom at a
section j. The arguments for area, contraction
coefficient, and other factors have been omitted to simplify
the notation. Solution of equation 106 for the flow gives
(107)
 ,
as the definition of FO flow.
,
as the definition of FO flow.
4.8.2 Free-Weir Flow
In order to maintain a smooth transition between FO flow and FW
flow, an equation similar to equation 106 is applied with the
assumption of critical flow at section 2 to define FW flow as
(108)
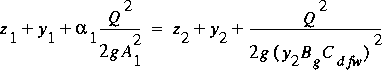 and
and
(109)
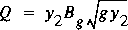 ,
,
where C dfw is the discharge coefficient for FW
flow. Substituting for flow in equation 108 with that from
equation 109 gives
(110)
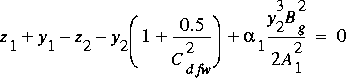 ,
,
as the nonlinear equation in the unknown water-surface height
at section 2. Equation 110 is solved iteratively for y
2 and then the flow through the sluice opening
is defined by equation 109.
4.8.3 Submerged-Orifice Flow
Two equations are required to define SO flow: an energy equation
analogous to equation 106 and a simple momentum balance. The
energy equation is
(111)
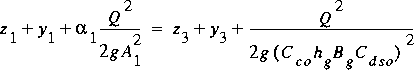 ,
,
where C dso is the discharge coefficient for SO
flow. The water-surface height at section 3 replaces the
piezometric level for the emerging jet, but the velocity head
is given by the velocity of the jet, assuming it is close to
the value that would have resulted had the jet not been
submerged. The simple momentum balance is
(112)
 ,
,
where the arguments of the first moment of area about the water
surface, J, have been shown explicitly. This equation
is applied for two purposes. In the first application, the
drop between sections 1 and 4 at the free-flow limit for FO flow
is defined. In this application, there is only one unknown,
y 4. The flow is defined in the FO
equation for the given upstream water-surface elevation at
section 1. In the second application, equations 111 and 112
are solved simultaneously to define the flow and the
submergence level, y 3, when the flows for
partial free drops are computed for a given value of y
1.
4.8.4 Submerged-Weir Flow
The energy equation for SW flow is
(113)
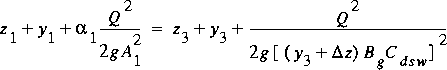 ,
,
where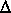 z is
z is
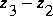 , and C dsw is the discharge coefficient for SW
flow. The corresponding momentum equation is
, and C dsw is the discharge coefficient for SW
flow. The corresponding momentum equation is
(114)
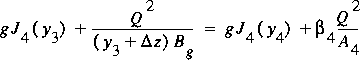 .
.
Equation 114 also is applied for the same two purposes as
equation 112 in the case of SO flow.
4.8.5 Outline of Solution Process for Underflow Gates
For each of a given series of gate openings, the free and
submerged flows must be computed for user-specified series of upstream water-surface elevations
and partial free drops (that specify the downstream water-surface elevations). For a given gate
opening, the following steps summarize the solution process.
-
The limiting upstream water-surface height for FW flow, y1fw, is determined for the gate opening. The FW flow is assumed to just touch the gate lip, that is, y2 = hg. The upstream water level required to produce the FW flow is computed from equation 108. The right-hand side (RHS) of equation 108 is known if y2=hg. Thus, the specific energy on the left-hand side may be used to compute the subcritical value of upstream water-surface height, y1fw. This water-surface height at section 1 defines h1fwul. The lower limit for FO flow, h1foll, is computed from h1fwul and hg. If all gate openings have been evaluated, the computations are complete.
-
The free flow for the current upstream water-surface height,
y 1, is determined if any upstream
water-surface heights must still be evaluated. If y
1
 y 1 fw, the
FW flow is computed for that level. If not, the FO flow is
computed for the current upstream water-surface height. The
free weir or orifice flow is denoted as Q f.
If no upstream water levels remain to be evaluated, the
procedure returns to step 1.
y 1 fw, the
FW flow is computed for that level. If not, the FO flow is
computed for the current upstream water-surface height. The
free weir or orifice flow is denoted as Q f.
If no upstream water levels remain to be evaluated, the
procedure returns to step 1.
2.1.
If the upstream water-surface elevation exceeds the
elevation of the gate lip (y1+z1>hg+z2), SW
flow will transition to SO flow. At the limiting
downstream water-surface-height level for SW flow,
y4sw, the water just
touches the gate lip from downstream. The flow rate
for this condition is computed with equation 113 with
y 3 = hg
+
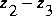
2.2.
The limiting downstream water-surface height for SW
flow, y4sw, is
calculated by solving
equation 114 for the tail-water
level, applying the value of y 3
and flow determined in step 2.1.
-
The downstream water-surface height at the free-flow limit,
y 4 f, is determined. If the
flow is FW, then equation 114 is applied to find y
4 f when the flow is Q f
and the water-surface elevation at section 3 matches the
water-surface elevation at critical flow at section 2.
Otherwise, y 4 f is computed
with equation 112 under the same conditions of matching
water levels at sections 2 and 3.
-
The next downstream water-surface height, y 4
, for submerged flow is computed. This is done on the
basis of distributing the partial free drops according to
parameters supplied by the user. The downstream water-surface height varies from the
free-flow limit to equality with the water-surface elevation at section 1.
-
If the flow is FO, the solution procedure moves to step 7;
otherwise, this step is done. For FW flow, the
submerged flow may be SW but may transition to SO if the
current upstream water-surface elevation is above the gate
opening. If y 1 + z
1 > h g + z
2, then steps 5.1 and 5.2 are done;
otherwise, step 6 is done.
5.1
If y 4 > y 4
sw, the submerged flow is SO. The SO flow is
computed applying equations 111 and 112. C co is
interpolated as needed to make the transition at the boundary
smooth.
5.2
If y 4  y 4
sw, the submerged flow is SW. The SW flow is
computed applying equations 113 and 114. The procedure returns
to step 4 for the next downstream water-surface height and the
computations continue.
y 4
sw, the submerged flow is SW. The SW flow is
computed applying equations 113 and 114. The procedure returns
to step 4 for the next downstream water-surface height and the
computations continue.
-
For this case, the FW flow can only transition to SW flow
for a constant upstream water-surface elevation. The SW
flow is computed applying equations 113 and 114. The
procedure returns to step 4 for the next downstream
water-surface height and the computations continue.
-
FO flow can only transition to SO flow for a constant
upstream water-surface elevation. The SO flow is computed
applying equations 111 and 112. The procedure returns to
step 4 for the next downstream water-surface height and the
computations continue.
This outline of the solution process suppresses the details of
storing the flows and the proper water-surface elevations in the
2-D tables. The computations are extensive, and many of the
equations must be solved using an iterative process such as
Newton's method or the method of false position. If 5 gate
openings and 15 upstream water-surface elevations are considered,
and 15 flows are computed for each upstream water-surface
elevation, then 1,125 values of flow must be computed with the
UFGATE command (section 5.20).
Precise definitions of the point of transition between the flow
regions in figure 16 are used in the solution procedure. These
transitions are not precise when observed in the field. The
level of submergence of the emerging jet required to affect the
flow during FO flow is unclear. The pressure distribution at
small levels of submergence of the jet is not hydrostatic. If
accurate field measurements are available to define this
transition, then the procedure can be modified to more
accurately define the point of transition. It also is assumed
in the transitions from weir flow that the critical depth, as
computed from 1-D flow theory, defines the contact with the
gate lip. This probably is not true. Streamline curvature as
the water approaches the gate opening will cause the pressure
distribution in the flow to deviate from hydrostatic. The
water surface will be strongly curved, and detailed knowledge
of the gate arrangement is needed to define the actual point of
contact. It also is possible that the point of transition from
FW to FO may differ from the point of transition from FO to FW.
The point of transition may depend on the direction of movement
of the water surface. Only careful measurements in the
laboratory or field can refine the assumptions applied here.
4.8.6 Interpolation for Flows at Nontabulated Gate Openings
Interpolation between tables of type 13 must be done to define the
flows at gate openings that fall between the gate openings
selected for the 2-D tables placed in the table of type 15.
Straightforward linear interpolation on the gate opening results
in large errors when the flow class changes within the interval of
interpolation. As an
example, if tables of type 13 have been computed at gate openings
of 2 and 3 ft, it is possible that interpolation at an opening of
2.5 ft would indicate FO flow in the table for the 2-ft opening
and FW flow in the table for the 3-ft opening. A means to
develop, conceptually at least, an intermediate table complete
with flow boundaries, computed from the tables below it and above
it in gate-opening sequence, is needed.
The approach for this interpolation is developed from a special
case of the governing equations. In this
special case the bottom elevation at all the key sections is
the same ( z 1 = z 2
= z 3 = z
4 ). Further, it is assumed that the approach and
departure sections are rectangular, that the contraction
coefficient is at most a function of the
piezometric head at section 1 relative to the gate opening, and
that  1 =
1 = 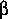 4
= 1. The gate-opening Froude number for orifice flow,
F g, is approximated as
4
= 1. The gate-opening Froude number for orifice flow,
F g, is approximated as
(115)
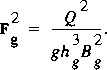
Applying this Froude number to describe the flow transforms the
governing equation for FO flow to
(116)
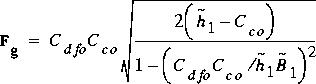 ,
,
where
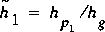 ,
, 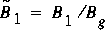 , and B 1 is the channel width at section 1.
In this form, the gate-opening Froude number is constant if the
gaterelative head at section 1 is a constant.
, and B 1 is the channel width at section 1.
In this form, the gate-opening Froude number is constant if the
gaterelative head at section 1 is a constant.
The conservation of energy equation for SO flow then becomes
(117)
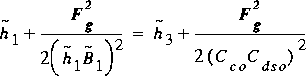 and the conservation of momentum equation becomes
and the conservation of momentum equation becomes
(118)
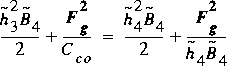 .
.
The symbols with the tilde are taken relative to the
corresponding dimension of the gate opening. These equations
indicate that the gate-opening Froude number is a constant if
the gate-opening relative heads at sections 1 and 4 are held
fixed.
If all sluice gates were accurately described with the
simplifying assumptions, then only one table of type 13 would
be needed to represent the flows for all nonzero gate openings.
This also implies that the boundaries between different flow
classes, expressed relative to the gate opening, would be
constant. Most sluice gates only approximately satisfy these
simplifying assumptions. The approach and departure sections
are only approximately
rectangular. Also, the bottom elevations are frequently not
all the same. A gate sill may be used to raise the gate
opening above the bottom of the approach channel. Furthermore,
it is often true that the bottom of the departure channel may
be below the gate opening to help stabilize the hydraulic jump.
These deviations from the simplifying assumptions cause (1) the
gate-opening Froude number to vary slightly even when the
gate-opening relative heads are held constant, and (2) the
boundaries between the flow regions to vary with gate opening.
The simplifying assumptions are even less appropriate for
tainter gates because, in addition to the problems at sluice
gates of varying bottom elevations for the approach and
departure sections and nonrectangular approach and departure
sections, the flow contraction coefficient varies with the lip
angle for tainter gates.
Because the simplifying assumptions previously described only
approximately apply to sluice gates and tainter gates, linear
interpolation is used on gate-opening relative values to
approximate the variations with gate opening in FEQ and FEQUTL.
In addition to the 2-D table number for each gate opening, type
15 tables contain three values that define key points on the
boundaries between the flow classes. These are the head at
section 1 at the upper limit of FW flow, the head at section 4
at the upper limit of FW flow, and the head at section 4 on the
boundary between SW and SO flow midway between heads at section
1 of h g and h 1 fwul
. These heads are all expressed relative to the gate opening.
The look-up procedure is as follows:
-
The interval in the type 15 table that contains the current
gate opening, h g, is determined. The table
with a gate opening less than h g, h gL
, is the left-hand table, and the table with a gate
opening greater than or equal to h g, h
gR is the right-hand table.
-
The three key points on the boundaries between flow regions
are interpolated with respect to gate opening. The
interpolated gate-opening ratios are then multiplied by hg
to obtain the actual values of h1fwul,
h4fwul, and h4swso.
-
If
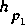 and
and
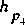 are in the weir-flow region, defined in figure 16, the
weir-flow values from the right-hand table are applied.
Otherwise, the procedure continues to step 4.
are in the weir-flow region, defined in figure 16, the
weir-flow values from the right-hand table are applied.
Otherwise, the procedure continues to step 4.
-
If this step is applied, the flow is orifice flow. The
heads used for interpolation in the tables are computed.
The heads at sections 1 and 4 for the left-hand table are
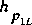 =
=
 and
and
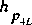 =
=
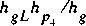 , respectively. The heads for the right-hand table are
computed in a similar manner for the right-hand gate opening.
, respectively. The heads for the right-hand table are
computed in a similar manner for the right-hand gate opening.
-
The flow rate is determined from each table, and the
gate-opening Froude number is computed for the left- and
right-hand tables. The gate width is taken as 1.0 for this
purpose. The actual width is not important.
-
Linear interpolation on gate opening is applied to compute
the gate-opening Froude number for hg. The
flow for the gate opening is then computed.
This approach for interpolating flow values for nontabulated gate
openings is more complex than simple
linear interpolation on gate opening, but errors resulting from
simple linear interpolation across the weir-flow and orifice-flow
boundary are avoided with few exceptions. The exceptions result
because linear interpolation for the boundary-point ratios are not
exact. Some mixed interpolations for orifice flow also may result
where one of the tables indicates SO flow and the other indicates
FO flow. This results close to the boundary and is caused by the
inexactness of linear interpolation in the tables. However, the
effect of these exceptions should be small if the flows of
interest are away from the boundaries between flow classes.
-
4.8.1 Free-Orifice Flow
-
4.8.2 Free-Weir Flow
-
4.8.3 Submerged-Orifice Flow
-
4.8.4 Submerged-Weir Flow
-
4.8.5 Outline of Solution Process for Underflow Gates
-
4.8.6 Interpolation for Flows at Nontabulated Gate
Openings
[Next Section]
[Previous Section]
[Table of Contents]
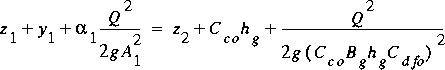 ,
, 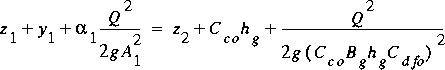 ,
,  ,
, 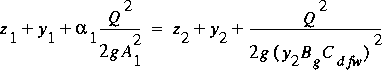
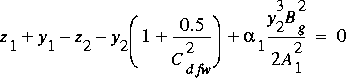 ,
, 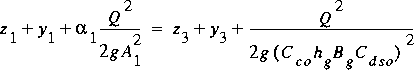 ,
,  ,
, 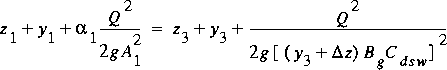 ,
, 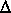 z is
z is
![]() , and C dsw is the discharge coefficient for SW
flow. The corresponding momentum equation is
, and C dsw is the discharge coefficient for SW
flow. The corresponding momentum equation is
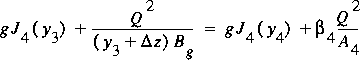 .
.  y 1 fw, the
FW flow is computed for that level. If not, the FO flow is
computed for the current upstream water-surface height. The
free weir or orifice flow is denoted as Q f.
If no upstream water levels remain to be evaluated, the
procedure returns to step 1.
y 1 fw, the
FW flow is computed for that level. If not, the FO flow is
computed for the current upstream water-surface height. The
free weir or orifice flow is denoted as Q f.
If no upstream water levels remain to be evaluated, the
procedure returns to step 1.
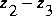
y 4 sw, the submerged flow is SW. The SW flow is computed applying equations 113 and 114. The procedure returns to step 4 for the next downstream water-surface height and the computations continue.
 1 =
1 = 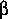 4
= 1. The gate-opening Froude number for orifice flow,
F g, is approximated as
4
= 1. The gate-opening Froude number for orifice flow,
F g, is approximated as
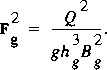
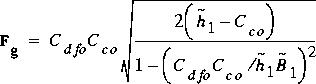 ,
, ![]() ,
, ![]() , and B 1 is the channel width at section 1.
In this form, the gate-opening Froude number is constant if the
gaterelative head at section 1 is a constant.
, and B 1 is the channel width at section 1.
In this form, the gate-opening Froude number is constant if the
gaterelative head at section 1 is a constant.
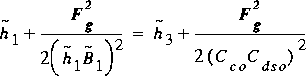
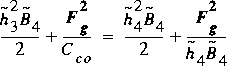 .
.