, defined as
Full Equations Utilities (FEQUTL) Model for the Approximation
of Hydraulic Characteristics of Open Channels and Control
Structures During Unsteady Flow
A generalization of the Ritter (1892) solution for the peak outflow following the instantaneous failure of a dam is computed with the GRITTER command (section 5.14). The reservoir cross section is assumed to be prismatic, horizontal, and frictionless. Furthermore, there can be an initial flow in the reservoir, and the cross section of the failure site need not match the cross section of the reservoir. Although restrictive, the assumptions for the generalized solution allow reasonable estimates to be made of the peak flows that are physically possible as a result of a variety of failures. These estimates can be used to assess the reasonableness of the results obtained through solution of the dam-break problem using the options available in FEQ.
The generalization to a nonrectangular channel cross section
involves the introduction of the Escoffier stage variable, , defined as
,
where
; The Escoffier stage variable transforms the characteristic form of the governing equations into a convenient form for solution. The details of this transformation and a derivation of the solution are presented in Franz (1977). The solution for the relation between the water-surface height and velocity at the dam site after the failure is
,
where
is the Escoffier stage variable at the dam site after the failure;Equation 101 contains two unknowns: water-surface height and water velocity at the dam site after the failure. If the dam fails completely and the cross section at the dam is identical to the cross section in the reservoir, the Ritter solution indicates that the flow at the dam site is critical. Thus, it is reasonable, as confirmed by test results, to assume that the flow at the dam site will be critical for a partial failure with perhaps some allowance made for the associated contraction losses. The critical-flow relation at the dam site for the dam breach provides another equation relating the velocity to water-surface height at the dam site in the reservoir cross section. Thus, a function, f DB ( y ), is defined that yields the flow through the breach for each water-surface height in the reservoir. The water-surface height in the reservoir is not the same as the water-surface height in the breach if the breach is partial. Therefore, f DB ( y ) gives the critical flow in the breach for the corresponding water-surface heights in the reservoir. In these calculations, it is assumed that the distance between the breach and the upstream point in the reservoir is a small part of the length of the reservoir and that the application of a steady-flow relation will not appreciably affect the results.
The depth and velocity in the reservoir at the dam site must be the same for both equation 101 and for f DB ( y ). Therefore, f DB ( y )/ A ( y ) is substituted for V D in equation 101 to yield the governing equation for the generalized Ritter solution as
. A modified false-position technique is applied to solve equation 102.
The command CRITQ (section 5.4) is designed to compute the function f DB ( y ), consistent with equations 100,101,102. The Escoffier stage variable is internally computed and interpolated in GRITTER by applying the following approximation to the integral in equation 100 over each tabulation interval in the cross-section table for the approach section
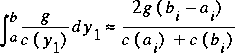, where a i and b i represent the limits of a tabulation interval in the cross-section table. This approximation is exact for rectangular, triangular, and parabolic cross sections as well as for any cross section that has a linear variation of hydraulic depth ( A/T ) with the maximum depth in the cross section.