Flow resistance coefficients, such as the Manning’s n, are used in a wide range of hydraulic and hydrologic analyses. The results of these analyses affect the design, operation, and management of water-resources projects. However, despite advancements in hydroscience theories and practices in general, determination of the n-values in natural environmental still is a challenge to engineers. This Web page is a source of n-values for streams of Illinois including both natural and artificial channels. All the n-values presented are determined from field data. The majority of the n-values data are collected from 2002 to present. In presenting the n-values, ancillary information, such as pictures of study reach and channels, site descriptions, is used to aid in the understanding of factors effecting n-values in Illinois streams. Users can apply the presented information to determine n-values at other sites of interest. This study of determining n-values for Illinois streams is conducted by the U.S. Geological Survey (USGS) in cooperation with the Illinois Department of Natural Resources – Office of Water Resources (IDNR-OWR).
A resistance coefficient is a measure reflecting the dynamic behavior, in terms of momentum
or energy, of roughness factors on the flow boundary in resisting the flow. A
roughness factor is a geometric measure reflecting the actual or effective
unevenness of the boundary (Yen, 2002). In computations, the
Manning’s equation relates the flow velocity, V, to n, as
Visual determination approach has been used by Fasken (1963), who compiled a guide for selecting the Kutter’s n-value (Chow, 1959) for drainage channels in various States in the country. Black and white pictures taken when the channels were at low flows and description of channels were presented (Fasken, 1963). Chow (1959) also listed photographs with typical n-values. As the slopes in equation 1 have to be determined from two or more locations in a reach, Barnes (1967) applied an equation (see equation 2) where n-values were computed as reach-wise averages. Reach-wise n-values from 50 streams in the country were presented along with color photographs and sketches of the cross sections, and site descriptions (Barnes, 1967). Barnes (1967) report has been recognized as a useful handbook for engineers in assigning Manning’s n-value because of the visual approach. Barnes studied stable channel sites and the reported n-values were computed with data collected after the occurrence of major floods. Photographs of the reach represent the conditions immediately after the flood. Since the publication of Barnes’ report, advancements have been made in understanding flow resistances such as examining the resistance coefficients using boundary layer theory in fluid mechanics, differentiating the momentum or energy approach in determining the resistance coefficients, describing the variation of n–values with depth/discharge using the composite and compound roughness elements and channel geometries, exploring n-values in alluvial streams, and others (Yen, 1991). There also are various efforts in extending Barnes’ visual approach for determining n-values in natural streams. For example, Hicks and Mason (1998) presented n-values for 78 New Zealand streams, Arcement and Schneider (1989) for floodplain channels, Coon (1998) for natural stream channels with vegetated banks, Gillen (1996) for streams in west-central Florida, Jarrett (1985) for high-gradient streams in Colorado, and Phillips and Ingersoll (1998) for natural and constructed channels in arid and semiarid environment in Arizona and other studies.
Variations in channel characteristics (geometry and bed or bank materials) because of hydrometerologic and/or physiographic patterns can lead to differences in n-values. Study sites have been selected in Illinois in order to include a variety of bed and bank materials, drainage areas, and channel geomorphologic characteristics. An initial planning matrix, based on natural channel and artificial bed and bank material and drainage areas, has been developed for guiding the selection of data-collection sites. Sites near or at USGS streamflow-gaging stations in the State are given higher priority because more information is available and more discharge measurements could be obtained. For reaches with no near-by gaging stations, sites selection is based primarily on visual inspection and field experience. Urban streams with artificial bed/bank treatments of interest also have been included in this study. Constructed streambeds and/or stream banks using fabricated materials, like gabion boxes, steel revetments, and concrete structures, are becoming more common in urban streams.
For the reach-wise n-value, at least three cross sections are needed if the study reach is reasonably straight and uniform; more cross sections are needed for more complicated reaches. Keeping the starting and ending cross sections similar is the basic requirement but this condition is difficult to follow sometimes. In this study, cross sections were surveyed by IDNR-OWR and USGS; or obtained from other Federal, State, local, and private agencies if recent surveys were available. Hydraulic properties, such as submerged area, hydraulic radius, and wetted perimeters, were computed from these cross sections for each study reach.
Discharge measurements were made using either conventional current meter methods (Rantz and others, 1982), or acoustic Doppler current profilers (ADCP) (Simpson, 2001).
For each n-value survey, water-surface elevations were measured by either
Slope stations consist of a base gage operated in conjunction with an auxiliary gage located upstream or downstream of the base gage. In addition, n-values were computed for six USGS streamflow-gaging stations in Illinois that are or were operated as slope stations. Discharge measurements at the six slope stations were retrieved from historical data during bank-full or less than bank-full conditions. Water-surface slope is computed using stages readings for the discharge at the base and auxiliary stations.
The n-values presented are "reach-wise" values. In the field, water-surface profiles are measured at least at two fixed points of a study reach. Therefore, the n-values should be specified for the reach, not for a cross section or a point. The reach-wise n-value used in numerical modeling and presented in the tables. Using one "representative cross section" to compute n-value from Manning's formula will have many uncertainties because of the possible errors with field measurements and engineering judgement Therefore, there are at least two cross sections involved in a reach-wise computation. In general, three or more cross sections are used to compute the reach-wise n-value. The hydraulic property data presented in the table, on the other hand, have to be averaged for these cross sections. Therefore, they cannot be used for back calculating of n-values collected in the field.
Equation 2 is used by Barnes (1967) and Jarrett and Petsch
(1985) in computing the n-value for a study reach where the flow can be
slightly non-uniform. The reach has multiple M cross sections designated
as 1, 2, … M-1, M
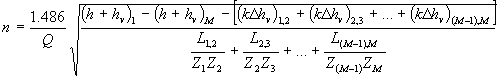
Each stream site is presented with headers and images of the site. This ancillary information is organized in the order of relative importance of the information to the users. The headers are explained in figure 1.
|
Location map: the study reach is identified with a red box on the USGS quadrangle map |
Cross sections used in the n-value computations are overlaid with aerial photograph and displayed with identification numbers. Aerial photographs that show clear, visual identification of channel types and other channel characteristics are used. |
|||
|
|
|
|
||
|
Shape of the cross sections used in the n-value computation. Cross sections are identified with identification numbers |
|
|||
|
Field photos taken at the time of measurement have the corresponding n-value marked. Arrangement is from low flows to high flows. |
(photo
presentation continues)
|
Four types of images are prepared for presenting the field data (figs. 1-2) The location of the study site is identified on the USGS quadrangle map. In addition, an aerial map that clearly shows the study site is used for illustrating the characteristics of the study reach. Cross-sectional shapes also are presented for reviewing the geometric factors. Locations of the cross sections are identified on the aerial photograph. Photographs of the channel were taken at the time of each the n-value survey. Bed and bank materials can be visualized during low-flow conditions. Ideally, four to five measurements under a wide range of flow conditions with accompanying photographs would be needed for a study site. The site photographs are annotated in the office with site name, view, date, and flow conditions. Later, the computed n-value is added to the corresponding picture. Photographs like these can be used to assist in understanding bed and bank, flow, and channel conditions.
A presentation template of n-values for Illinois streams is illustrated in figure 1; an example Web presentation is illustrated in figure 2. Besides the images, four headers are used for describing the study reach and site characteristics. Because of space limitations, text descriptions under headers are not shown.