Update for section 4.2.5 Departure-Reach Losses, Franz and Melching(1997b), p.55
Section 4.2.5 Departure Reach Losses
 |
Bodhaine(1968) takes the departure reach losses to be complete loss of the velocity head difference between the culvert exit and the departure section. This loss is in general too large. The cumulative effect of using this simple loss on a sequence of culverts along a stream in an urban area could seriously bias the water-surface elevations. Therefore, FEQUTL uses a simple momentum balance in the departure reach following Henderson (1966, pp. 208-210). This approach or variations of it have been used by Schneider and others (1977). |
 |
A simple momentum balance assumes that the departure reach is horizontal, prismatic, and frictionless. FEQUTL represents the simple momentum balance using sections 3, 43, 44, and 4 as shown in Fiq. 4-1. Section 43, the cross section of the stream channel a short distance downstream of the culvert exit represents the upstream end of the control volume for the simple momentum balance. Section 44 represents the downstream end of the control volume for the simple momentum balance. Because friction and bottom slope are ignored, the distance between these two sections does not enter the computations. Section 44 is always the same as section 43 because the simple momentum balance assumes a prismatic channel. Different designations are used because the water-surface elevation and depth of water in these sections will differ. If the departure reach is in fact prismatic and horizontal, section 4 will be the same as sections 44 and 43 and will have the same water surface elevation as section 44. |
 |
If the departure reach is not horizontal or not prismatic, then section 4 will differ from section 43. However, section 44 will still be the same as section 43, creating a horizontal and prismatic sub-reach for the departure reach. This is needed for the simple momentum balance. A simple momentum balance is used to estimate the losses in this case also because the application of the momentum balance to a non-horizontal or non-prismatic control volume requires knowledge of the water-surface profile in the control volume. Simple assumptions as to the nature of this profile introduce errors so large as to make the results useless. This is analogous to the representation of a hydraulic jump. A simple momentum balance produces a close match to measurements so long as the jump occurs in a prismatic nearly horizontal channel. As soon as the channel becomes non-prismatic or non-horizontal, simple estimation of the gravity force or of the downstream component of the pressure forces on the sides of the channel fails to produce good results. Recourse must be had to laboratory measurements. No such measurements exist for the departure reaches of culverts and only for a limited number of cases for hydraulic jumps. |
 |
With these assumptions outlined, let momentum
flux over the roadway; momentum
flux over the roadway;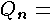 the
flow at a given section with section number the
flow at a given section with section number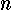 ; ; 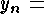 the
maximum depth of water in section number the
maximum depth of water in section number 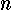 ; ; 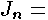 the
first moment of area about the water surface at section the
first moment of area about the water surface at section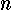 ; ; 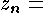 elevation
of the minimum point in section number elevation
of the minimum point in section number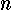 ; ; 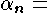 kinetic
energy flux correction coefficient in section kinetic
energy flux correction coefficient in section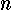 ; ; 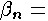 momentum
flux correction coefficient in section momentum
flux correction coefficient in section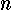 ;
and ;
and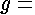 acceleration
due to gravity. Then the simple energy balance between sections 4 and 44
is: acceleration
due to gravity. Then the simple energy balance between sections 4 and 44
is: |
 |
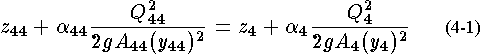  .
Equation
4-1 transfers the water surface elevation at section 4 to section 44 assuming
no energy losses. The simple momentum balance becomes .
Equation
4-1 transfers the water surface elevation at section 4 to section 44 assuming
no energy losses. The simple momentum balance becomes |
 |
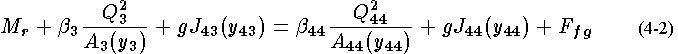 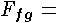 drag
force for a flapgate. drag
force for a flapgate. |
 |
The conversion of a head loss to a drag force follows the discussion in Franz and Melching (1997a), section 5.5.2 under the section: "Transformation of energy-head losses to drag forces for control structures". The drag force for a flapgate must be estimated from available published analyses. Nagler (1923) published a design chart based on the results from 18-inch, 25-inch, and 30-inch diameter gates. (it should be noted that flapgates are constructed with greater mass today than in the 1920's). The tests are assumed to be made with the pipe flowing full and a submerged exit, because it is recommended that the design chart be used for submerged flow conditions and that head-loss data for free discharge are not available. The following equation is also from Nagler (1923). |
 |
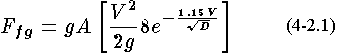 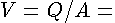 mean
velocity in the conduit; mean
velocity in the conduit;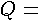 flowrate
in the conduit; flowrate
in the conduit; 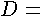 ,
vertical
diameter of the conduit; and ,
vertical
diameter of the conduit; and 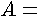 flow
area in the conduit. The original reference, Nagler(1923), is not available
to me, but I assume that the tests were made with the pipe flowing full
and with the exit always completely under water. The term in square brackets
in Eq. 4-2.1 is the head-loss term. flow
area in the conduit. The original reference, Nagler(1923), is not available
to me, but I assume that the tests were made with the pipe flowing full
and with the exit always completely under water. The term in square brackets
in Eq. 4-2.1 is the head-loss term. |
 |
We have extended the use of the equation in the following way for the CULVERT command: |
 |
1. The effect of the flapgate is applied to all submerged flows: full and part full. The velocity head is computed as if the pipe were flowing full and the full area is used in computing the drag force. This means that the part-full submerged losses are much smaller than the full-flow submerged losses. We include all levels of submerged flow to avoid abrupt changes in the loss relationship. These changes lead to rapid shifts in the flow relationship that appear unrealistic. |
 |
2. No loss is applied to any free flow: full or part full. There are probably some losses but they are generally assumed to be less than the losses for submerged flow. A complete cogent analysis with supporting laboratory or field measurements has not been found. |
 |
3. The culvert command makes no attempt to compute the head difference required to open a flap gate. To do so would require detailed information on the weight of the gate, the hinge arrangements, the angle that the gate seat makes with the vertical, and probably some empirical factors. |
 |
Equations 4-1 and 4-2 give the relationships for the departure reach once the culvert and roadway flows and momentum fluxes are known. |
![]() Back
to Franz and Melching(1997b), p.55, for section 4.2.5, Departure-Reach
Losses
Back
to Franz and Melching(1997b), p.55, for section 4.2.5, Departure-Reach
Losses