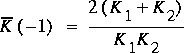[Next Section]
[Previous Section]
[Table of Contents]
Full Equations Utilities (FEQUTL) Model for the Approximation of Hydraulic Characteristics of Open Channels and Control Structures During Unsteady Flow
U.S. GEOLOGICAL SURVEY WATER-RESOURCES INVESTIGATIONS REPORT 97-4037
3.2 Channel Expansions and Contractions
The expansions and contractions considered in this section are
large enough that critical controls may be present or are located
at a junction among branches. The eddy losses at minor variations
in channel shape and size can be represented within a branch (see
section 5.5.3 in the documentation report for the Full Equations
model (Franz and Melching, 1997)). The expansions and
contractions considered here may result from both natural and
constructed changes of channel cross-sectional shape.
A 2-D table of type 14 is computed in the EXPCON
command (section 5.7) in FEQUTL to approximate the flow through
a transition in channel cross-sectional shape. The transition
is defined by an upstream cross section, a downstream cross
section, the respective bottom elevations, the distance between
the cross sections, and parameters related to the computation
of friction and shock losses. Flow through a channel
transition is a complex
phenomenon, and evaluation of losses is difficult.
The shock losses are approximated in EXPCON
by a constant fraction of the difference in the true velocity
heads where the constant differs for contracting and expanding
flows. This approximation has been frequently used in
hydraulic engineering, and most handbooks have recommended
ranges for the loss coefficients. The approximation is crude,
but no suitable replacement is readily available.
The principal difficulty with flows in transitions is that the
velocity distribution changes from section to
section in a manner only slightly affected by the channel
boundary. This is especially true of expanding flows with
possible channel-wall-separation effects and the attendant,
inherent instability in the velocity distribution. This
unpredictable variation in velocity distribution makes
estimation of the losses difficult. Simplifying assumptions
are made in the EXPCON command so that flow
computation is possible. Some of the major assumptions are
given below.
- The velocity-head (energy-flux) correction factor,
 , for both the upstream and downstream sections, is a
function of depth in the section and is computed in the
cross-section table commands in FEQUTL. This means the
velocity distribution is determined by the boundary geometry
alone. This is only approximately correct and may be
substantially incorrect if the transition is an expansion.
However, little other choice is available for reasonably
determining flow through the transition without making each
transition a research project.
, for both the upstream and downstream sections, is a
function of depth in the section and is computed in the
cross-section table commands in FEQUTL. This means the
velocity distribution is determined by the boundary geometry
alone. This is only approximately correct and may be
substantially incorrect if the transition is an expansion.
However, little other choice is available for reasonably
determining flow through the transition without making each
transition a research project.
- The pressure distribution at both the upstream and
downstream cross sections is hydrostatic. This should be
satisfied so long as the sections are away from regions with
pronounced vertical or horizontal curvature (or
acceleration).
- The losses resulting from boundary friction can be estimated
by a mean friction slope multiplied by the distance between
the two sections. Several options are available for
computing the mean friction slope. The user also may
request that boundary-friction losses be ignored in the
computations. Given the uncertainties of the loss
estimation, ignoring the boundary-friction losses is often a
reasonable option.
- Control by critical depth will be located at either the
upstream section or the downstream section. The possibility
that the control is at some intermediate point is ignored.
Determination of the location of the actual control point in
a transition is difficult, and again the uncertainties
inherent in the calculation of flows in transitions do not
justify the additional effort and assumptions required to
determine the location of a control at an intermediate
point. In any case, it is unlikely that the control would
remain at an intermediate point over more than a narrow
range of flows. Thus, although such a control is possible,
it is unlikely to practically affect flows at the level of
detail of interest in applications of FEQ.
- Critical flow is as defined in the cross-section tables
computed in FEQUTL. The critical-flow value is affected by
the choice of parameters when the cross-section table is
computed. Application of the NEWBETA option(sections 5.8 and 5.9) will produce results
that differ from those produced without its application. A
critical-flow value that reflects the effect of velocity
distribution is computed in the NEWBETA
option. In all other cases, critical flow is
computed as if the velocity distribution were uniform across
the cross section and
 =
= 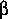 = 1. Thus, if the
channels under consideration are not compact, then
NEWBETA should be applied. The critical flow in closed
conduits with flow transitions must be limited by
application of the QCLIMIT command (section 5.18)
before the EXPCON command is invoked.
= 1. Thus, if the
channels under consideration are not compact, then
NEWBETA should be applied. The critical flow in closed
conduits with flow transitions must be limited by
application of the QCLIMIT command (section 5.18)
before the EXPCON command is invoked.
- Critical flow is meaningful in a flow transition, and the
water-surface curvature introduced may invalidate the
assumption of hydrostatic pressure distribution. However,
the transitions often are short and the often-substantial water-surface curvature resulting from critical
flow in the transition may not affect the computations in
FEQUTL. A further problem is that critical flow may result
at the downstream section even though the flow is expanding
in a situation where the flow area at the critical section
is larger than the flow area upstream. If the cross-section
shapes were the same, then this situation would not be
possible. However, changes in cross-section shape also may
be simulated in EXPCON. When the cross-section
shape changes in the transition, critical flow can result at
the section with the larger area in FEQUTL computations.
- Computation of the losses in the transition in channel
cross-sectional shape as a fraction of the difference in
velocity heads between upstream and downstream sections
applies in the limit as flow becomes critical. The formula
of head loss as a function of velocity-head difference was
derived for subcritical flows not close to critical because
most designs of transitions in cross-sectional shape avoid
flows near critical.
- The loss formula can be smoothed to represent losses when
the flow areas are nearly the same but the cross-section
shapes are not. The uncorrected formula results in a zero
loss at that point. Some losses must result because the
change in shape can be large even though the flow areas are
the same. This illustrates a deficiency of applying any
formula that depends on velocity or velocity head
differences alone. Again, little alternative is available
to this approach, and smoothing over this region as outlined
in the following section results in losses that are
consistent with the simple loss formula.
3.2.1 Governing Equations for Expansions and Contractions
The principal equation used to estimate the flows in a transition is
(72)
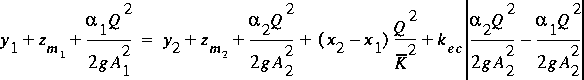 ,
,
where zm is the elevation of the minimum
point,
 is the mean conveyance, x is the
location of the section along the channel, and kec is the loss factor depending on the sense of the
transition. The sense of the transition denotes whether the
flow is expanding or contracting. Another convenient and
perhaps preferable description is to define the flow in the
transition as either accelerating or decelerating. The flow is
accelerating in a contraction and
decelerating otherwise. The subscripts denote the section with
section 1 the upstream section and section 2 the downstream
section of the transition.
is the mean conveyance, x is the
location of the section along the channel, and kec is the loss factor depending on the sense of the
transition. The sense of the transition denotes whether the
flow is expanding or contracting. Another convenient and
perhaps preferable description is to define the flow in the
transition as either accelerating or decelerating. The flow is
accelerating in a contraction and
decelerating otherwise. The subscripts denote the section with
section 1 the upstream section and section 2 the downstream
section of the transition.
Equation 72 is applied to critical flow despite the potential
problems outlined previously. The need to compute critical
flow results primarily from the requirement for a consistent
flow in FEQ simulations. Therefore, the flow relations must
include the possibility of critical control even though the
user believes such flow will not result. The purpose of
modeling is to understand the behavior of a proposed or real
stream system and to make reasoned estimates for conditions for
which no data are available (for example, design conditions and
extreme conditions for planning scenarios). Simulation of
these conditions may unintentionally impose flows and depths
that result in critical control at one or more locations where
such a control is possible. If FEQ does not include that
possibility, the computations either will fail for some unknown
reason or will yield an unreasonable result because the control
present in the structure is not simulated. Furthermore, if
such a control appears unavoidable, some change in the physical
structure should be made so that critical flow can be estimated
more accurately. If this is not possible, a physical model
must be constructed to define the flow and its characteristics
at that location in the stream.
Consistent and reasonable estimates of critical flow, within
the bounds of 1-D analysis, are required. For those cases in
which critical flow is difficult to define, assumptions must be
made as needed to produce consistent relations for the flow
through the transition. The assumptions applied in FEQUTL
computations of flow in transitions have been described in this
section.
3.2.2 Expansion-Contraction Losses
The computation of expansion-contraction losses (eddy losses or
shock losses) is approximate and uncertain. In general, the loss
fraction for expanding flows commonly is considerably larger than
for contracting flows. No problems result if the sense of the
transition never changes. However, when the sense of the
transition changes, patterns of flow may result such that the
velocity head change is small, but the flow undergoes a major
change in section shape. A computational point may result in the
flow simulation where the velocity heads on each side of the
transition are the same and no energy loss will be estimated with
equation 72. The user has the option of requesting smoothing of
the loss formula near this point to provide some loss at this
point. The loss term can be exactly computed as
(73)
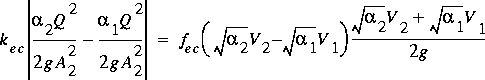 ,
,
where Vis the average velocity in the cross section (=Q/A). The function, fec(X), is defined as XkA when
X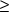 0 and as -XkD when
X< 0, where kA is the loss coefficient for accelerating (contracting)
flows, kD is the loss coefficient for
decelerating (expanding) flows, and X is the
difference in the product of the velocity and the energy-flux
correction coefficient from the downstream section to the
upstream section (difference in the rescaled velocities). For
equation 73 to be valid for both transition senses, fec (X) must be greater than or equal to zero.
No information is available on the loss coefficients when the
kinetic-energy-flux correction factor is large. In equation
73, it is assumed that the loss should be proportional to the
difference in the true velocity head and not in the nominal
velocity head. The sense of the loss is assumed to change at
the zero difference point between the rescaled
velocities, the argument to the function fec.
Smoothing this function when the argument is near zero will
result in a loss when the difference in velocity heads is zero.
0 and as -XkD when
X< 0, where kA is the loss coefficient for accelerating (contracting)
flows, kD is the loss coefficient for
decelerating (expanding) flows, and X is the
difference in the product of the velocity and the energy-flux
correction coefficient from the downstream section to the
upstream section (difference in the rescaled velocities). For
equation 73 to be valid for both transition senses, fec (X) must be greater than or equal to zero.
No information is available on the loss coefficients when the
kinetic-energy-flux correction factor is large. In equation
73, it is assumed that the loss should be proportional to the
difference in the true velocity head and not in the nominal
velocity head. The sense of the loss is assumed to change at
the zero difference point between the rescaled
velocities, the argument to the function fec.
Smoothing this function when the argument is near zero will
result in a loss when the difference in velocity heads is zero.
A small, positive value of velocity difference, denoted by 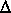 V, is specified by the user to define an interval,
[-
V, is specified by the user to define an interval,
[-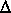 V,
V, 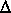 V]. Over this interval, a
cubic polynomial is fitted such that the value of the function
and its derivative is matched by the polynomial and its
derivative at the ends of the interval. Under these
conditions, the coefficient on the cubic term in the polynomial
vanishes and a parabolic transition over the interval is
obtained, yielding
V]. Over this interval, a
cubic polynomial is fitted such that the value of the function
and its derivative is matched by the polynomial and its
derivative at the ends of the interval. Under these
conditions, the coefficient on the cubic term in the polynomial
vanishes and a parabolic transition over the interval is
obtained, yielding
(74)
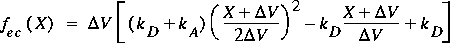 .
.
This smoothing procedure yields a function with a continuous first derivative over the entire range. Without smoothing, the derivative of fec is discontinuous at the origin. At the origin, the point of zero loss without smoothing, the smoothed function yields
 .
.
This means that, when the velocity difference is zero, the loss
is estimated to be the same as the loss that would result from
a velocity difference of 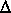 V and a loss
coefficient that is one-half the average of the two loss
coefficients.
V and a loss
coefficient that is one-half the average of the two loss
coefficients.
3.2.3 Mean Conveyance for the Expansion or Contraction
The friction losses defined in equation 72 depend on the method
for computing a mean conveyance. The mean conveyance is defined
as a function of an averaging parameter, a, as
(75)
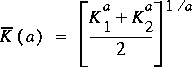 .
.
The generalized mean for two values is given by equation 75.
The mean values obtained as a varies over its range
are
(76)
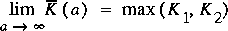
(77)
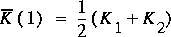
(78)

(79)
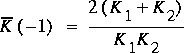
(80)
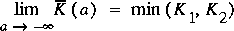 .
.
Equation 77 gives the arithmetic mean, equation 78 gives the
geometric mean, and equation 79 gives the harmonic mean of the
two end-point conveyances. No established rules are available
regarding which mean value to apply. The geometric mean is
preferred in many cases and may be a reasonable first
approximation.
3.2.4 Outline of Solution Process for Expansions and Contractions
The user specifies a series of downstream piezometric heads to
define the 2-D table of type 14. The head is measured from the
maximum of the two bottom elevations for the cross sections at
each end of the transition. For each downstream head, the
upstream piezometric head resulting in critical flow at either
cross section must be computed with the EXPCON command
(section 5.7). This defines the smallest critical flow that can
result for the given downstream head. The upstream piezometric
head is computed as a function of downstream head and partial free
flow for a series of partial free flows (critical flow is the free
flow) until the partial free flow is zero. When the partial free
flow is zero the two heads are equal. Each stage of the
computations involves an iterative solution.
A control may result at either cross section and the control
may shift as the flow levels change. An
extensive search is made in EXPCON computations for a
control at each of the cross sections, if necessary. The
validity of this control is checked in EXPCON
computations. For a control to be valid, the flow must be
critical at one section and subcritical at the other section.
It may be that no control can be found. Normally, this problem
can be solved by adjustment of the friction losses. In some
cases, the addition of a small friction loss allows a control
to be found in the computations. In other cases, the reduction
or elimination of friction loss allows a control to be found in
the computations.
Special care must be applied if a closed conduit is present in
the flow transition; for example, a stream directed underground
through a long, closed conduit of substantially different
cross-sectional area. Critical flow is undefined when a closed
conduit is flowing full. The introduction of a hypothetical
slot in the top of the conduit allows a hypothetical,
equivalent free surface to be simulated to account for
pressurized flow, but leads to a critical flow, which commonly
is many times larger than any flow that may result in the
conduit. This results in unrealistic upstream heads in the
computations. These large heads cause only a small part of the
table to be utilized in FEQ simulations. To avoid this
unrealistic outcome, the QCLIMIT command (section
5.18) should be applied to the closed-conduit cross section or
cross sections before EXPCON is invoked for those
sections. The critical flows tabulated in the cross-section
table are modified in QCLIMIT so that the maximum
value is more realistic, although arbitrary. For accurate and
reliable simulation, the maximum flow assigned to the critical
flow when the closed conduit is full must be somewhat larger
than the maximum flow likely to result in the conduit.
- 3.2.1 Governing Equations for Expansions and Contractions
- 3.2.2 Expansion-Contraction Losses
- 3.2.3 Mean Conveyance for the Expansion or Contraction
- 3.2.4 Outline of Solution Process for Expansions and Contractions
[Next Section]
[Previous Section]
[Table of Contents]
 , for both the upstream and downstream sections, is a
function of depth in the section and is computed in the
cross-section table commands in FEQUTL. This means the
velocity distribution is determined by the boundary geometry
alone. This is only approximately correct and may be
substantially incorrect if the transition is an expansion.
However, little other choice is available for reasonably
determining flow through the transition without making each
transition a research project.
, for both the upstream and downstream sections, is a
function of depth in the section and is computed in the
cross-section table commands in FEQUTL. This means the
velocity distribution is determined by the boundary geometry
alone. This is only approximately correct and may be
substantially incorrect if the transition is an expansion.
However, little other choice is available for reasonably
determining flow through the transition without making each
transition a research project. =
= 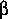 = 1. Thus, if the
channels under consideration are not compact, then
NEWBETA should be applied. The critical flow in closed
conduits with flow transitions must be limited by
application of the QCLIMIT command (section 5.18)
before the EXPCON command is invoked.
= 1. Thus, if the
channels under consideration are not compact, then
NEWBETA should be applied. The critical flow in closed
conduits with flow transitions must be limited by
application of the QCLIMIT command (section 5.18)
before the EXPCON command is invoked.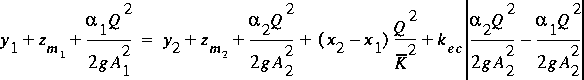 ,
,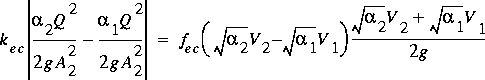 ,
, 0 and as -XkD when
X< 0, where kA is the loss coefficient for accelerating (contracting)
flows, kD is the loss coefficient for
decelerating (expanding) flows, and X is the
difference in the product of the velocity and the energy-flux
correction coefficient from the downstream section to the
upstream section (difference in the rescaled velocities). For
equation 73 to be valid for both transition senses, fec (X) must be greater than or equal to zero.
No information is available on the loss coefficients when the
kinetic-energy-flux correction factor is large. In equation
73, it is assumed that the loss should be proportional to the
difference in the true velocity head and not in the nominal
velocity head. The sense of the loss is assumed to change at
the zero difference point between the rescaled
velocities, the argument to the function fec.
Smoothing this function when the argument is near zero will
result in a loss when the difference in velocity heads is zero.
0 and as -XkD when
X< 0, where kA is the loss coefficient for accelerating (contracting)
flows, kD is the loss coefficient for
decelerating (expanding) flows, and X is the
difference in the product of the velocity and the energy-flux
correction coefficient from the downstream section to the
upstream section (difference in the rescaled velocities). For
equation 73 to be valid for both transition senses, fec (X) must be greater than or equal to zero.
No information is available on the loss coefficients when the
kinetic-energy-flux correction factor is large. In equation
73, it is assumed that the loss should be proportional to the
difference in the true velocity head and not in the nominal
velocity head. The sense of the loss is assumed to change at
the zero difference point between the rescaled
velocities, the argument to the function fec.
Smoothing this function when the argument is near zero will
result in a loss when the difference in velocity heads is zero. V, is specified by the user to define an interval,
[-
V, is specified by the user to define an interval,
[-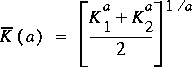 .
.